前言
Strassen最早于1968年由Volker Srassen发表于论文《Gaussian Elimination is not Optimal》,将矩阵乘法的算法复杂度首次从O(n3),where log2(8)=3降低到O(n2.807),where log2(7)≈2.807。后来有不同的方法基于此算法进行改进。
MNN Strassenconv1x1采用的是2008年发表的这边文章中的算法《Memory efficient scheduling of Strassen-Winograd’s matrix multiplication algorithm》,主要针对memory访问上进行优化。
原理
普通矩阵乘
以C=AB为例,假设A和B均为n×n矩阵,则C中每个元素需要通过以下方式计算:
cij=k=1∑naikbkj
即每个元素计算需要n次乘法,n−1次加法,C共有n2个元素,故一共需要n3次乘法和n2(n−1)次加法,故算法复杂度为O(n3)。
分治法
Strassen算法基于分治的思想,因此我们首先考虑一个简单的分治策略。
假设矩阵A和矩阵B都是n×n,(n=2k)的方阵,求C=AB,则每个n×n的矩阵都可以分割为四个(n/2)×(n/2)的矩阵:
A=[A11A21A12A22] B=[B11B21B12B22] C=[C11C21C12C22]
于是C=AB可以改写为:
[C11C21C12C22]=[A11A21A12A22][B11B21B12B22]
展开有:
C11=A11B11+A12B21C12=A11B12+A12B22C21=A21B11+A22B21C22=A21B12+A22B22
每个等式需要两次矩阵乘法和一次矩阵加法。若用T(n)表示两个n×n矩阵之间的乘法,则有如下递归式:
T(n)=8T(2n)+Θ(n2)
其中:
-
- 8T(2n)表示8次子矩阵乘法,子矩阵规模为(n/2)×(n/2);
-
- Θ(n2)表示4次子矩阵加法以及合并C矩阵的时间复杂度。
根据递归式求解,得T(n)=Θ(nlog28)=Θ(n3),与普通矩阵乘的时间复杂度相同。分治法并不能起到加速的效果。
原始版本Strassen
分治法包含了8次矩阵相乘和4次矩阵相加,相比矩阵加法,矩阵乘法是非常慢的。这8次矩阵相乘正是瓶颈的来源。于是我们想到能不能减少矩阵相乘的次数,哪怕代价是更多的矩阵相加。Strassen正是利用了这一点。
-
- 同样还是每个矩阵分成4份,然后创建如下10个中间矩阵(10次矩阵加法10×2n×2n,时间复杂度为Θ(n2)):
S1=B12−B22S2=A11+A12S3=A21+A22S4=B21−B11S5=A11+A22S6=B11+B22S7=A12−A22S8=B21+B22S9=A11−A21S10=B11+B12
-
- 而后是执行7次矩阵乘法(时间复杂度7T(2n)=Θ(nlog27)=Θ(n2.807)):
P1=A11S1P2=S2B22P3=S3B11P4=A22S4p5=S5S6P6=S7S8P7=S9S10
-
- 最后通过这7个矩阵计算得到C矩阵(8次矩阵加法8×2n×2n,时间复杂度Θ(n2)):
C11=P5+P4−P2+P6C12=P1+P2C21=P3+P4C22=P5+P1−P3−P7
综合可得如下递归式:
T(n)={Θ(1)7T(2n)Θ(n2)if n=1if n>1
进而总的时间复杂度为T(n)=Θ(nlog27)=Θ(n2.807)
改进版本Strassen
S1=A21+A22T1=B12−B11S2=S1−A11T2=B22−T1S3=A11−A21T3=B22−B12S4=A12−S2T4=T2−B21
P1=A11B11P2=A12B21P3=S4B22P4=A22T4P5=S1T1P6=S2T2P7=S3T3
U1=P1+P2U5=U4+P3U2=P1+P6U6=U3−P4U3=U2+P7U7=U3+P5U4=U2+P5
C=[U1U6U5U7]
改进版本的Strassen相比原始版本矩阵加法次数由18次降低到15次。同时该算法同时分析各中间矩阵块之间的依赖关系,充分考虑到了计算中的内存复用,每次递归只需要动态分配两块临时内存X1,X2即可,C11,C12,C21,C22都可以在计算中复用。
计算流程图如下:
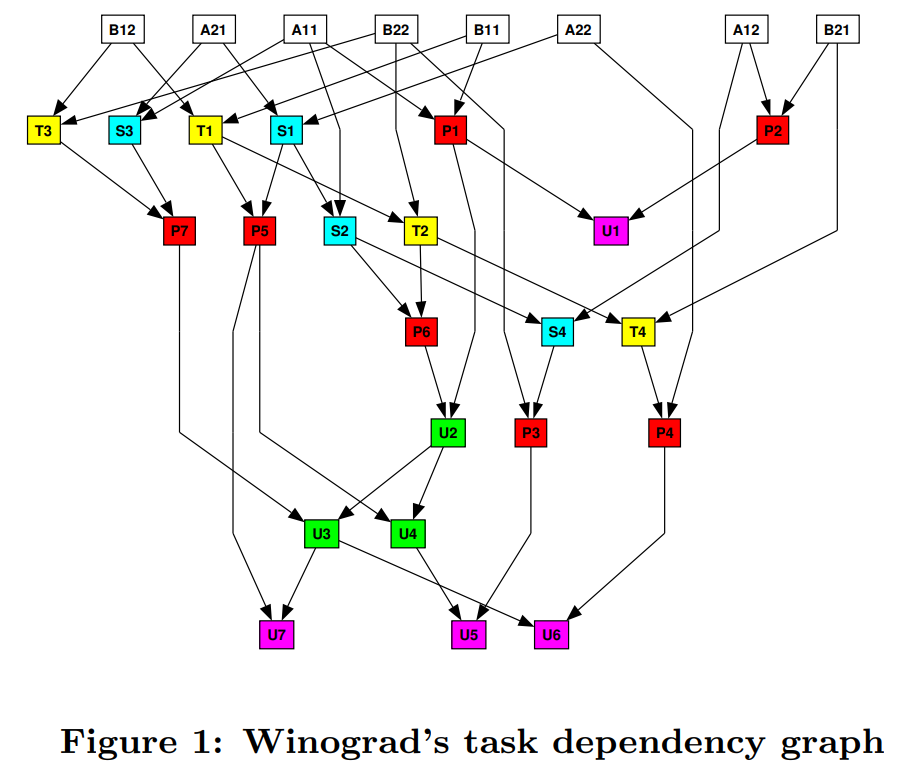
计算流程表如下:

总结
Strassen优化原理是减少矩阵乘法,额外增加的是更多矩阵加法,矩阵乘法的时间复杂度O(n3),而矩阵加法的复杂度是O(n2)。总体上乘加运算次数是减少的,来达到加速目的。
下图展示了普通矩阵乘法和Strassen算法的性能差异,n越大,Strassen算法节约的时间越多。
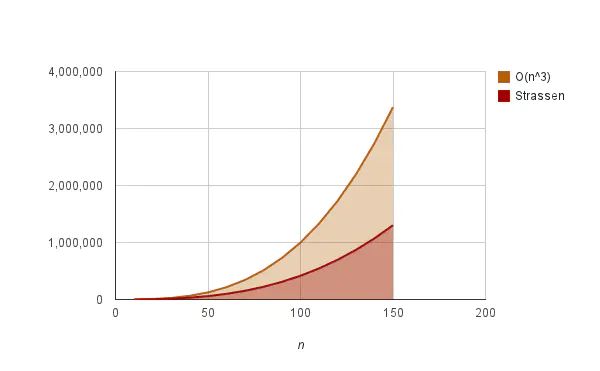
实际使用中,考虑到每次递归计算分块矩阵的访存问题,会与普通矩阵乘法的做一个cost比较,满足一定条件下切换到普通矩阵乘法,终止递归。
参考
致谢
文章主体框架参考自东哥的MNN源码解读的内部分享,加上了自己的一些看法。有幸被看到的话,希望能给点个赞~~











![现代硬件算法[8.8]: 时空局部性](/images/pd_09.webp)
![现代硬件算法[8.7]: 缓存遗忘算法](/images/pd_08.webp)
![现代硬件算法[8.6]: 淘汰策略](/images/pd_07.webp)
![现代硬件算法[8.5]: 列表排名](/images/pd_06.webp)
![现代硬件算法[8.4]: 外部排序](/images/pd_05.webp)