时空局部性

要精确评估算法在内存操作方面的性能，我们需要考虑缓存系统的多个特性：缓存层的数量，每层的缓存大小和块大小，每层用于缓存淘汰的具体策略，有时甚至需要考虑内存分页机制的细节。

在设计算法的初期阶段，应该尽可能地抽象这些细节，而不是计算理论的缓存命中率。这是因为更定性地去思考缓存性能，通常更有意义，也更有助于理解和改善算法性能。

在这个背景下，用来讨论缓存重用程度的方式主要有两种：

时间局部性（Temporal locality）是指在一小段时间内反复访问同一数据，使得在连续的请求之间，这份数据能够继续存储在缓存中；
空间局部性（Spatial locality）是指访问的数据如果在内存中地址相邻，那么它们可能在同一内存块中被一起获取，这样也能提高数据获取的效率。简单来说，就是"正在使用的数据附近的数据，接下来可能会被用到"。

换句话说，时间局部性是指这个相同的内存位置很可能很快就会再次被请求，而空间局部性是指一个附近的位置很可能在此之后马上被请求。

在本文种，我们将进行一些案例研究，以展示这些高级概念如何在实际优化中提供帮助。

深度优先与广度优先

考虑一个分而治之的算法，比如归并排序。它有两种实现方法：

我们可以递归地实现它，或者叫“深度优先”，这是通常的实现方式：先排序左半部分，再排序右半部分，然后合并结果。
我们也可以迭代地实现它，或者叫“广度优先”：先处理数据集的最底层，遍历整个数据集，并将奇数元素和偶数元素进行比较，然后将第一对元素和第二对元素合并，将第三对元素和第四对元素合并，依此类推。即先处理所有的单个元素，然后合并相邻的元素，逐步合并成更大的部分，直到整个数据集都处理完毕。

看起来迭代实现起来更麻烦，但更快——因为递归总是慢的，对吗？

一般来说，递归确实会慢，但是对于归并排序和许多类似的分治算法来说，情况并非如此。尽管迭代方式有其优势，例如只进行顺序的I/O操作，但是递归方式在时间局部性上表现更好：当一个数据片段可以完全放入缓存时，它会在之后所有的递归操作中被一直保留在缓存中。这样，随着操作的深入，虽然每一层的递归执行速度可能会有所下降，但整体上因为利用了缓存，递归方式在整体访问时间上可能反而更短，性能更好。

实际上，由于我们只需要做 $O(\log \frac{N}{M})$ 次数组拆分就可以将数据片段完全放入缓存，所以我们总共只需要读取 $O(\frac{N}{B} \log \frac{N}{M})$ 个块。而在迭代方法中，无论如何整个数组都会被重新读取 $O(\log N)$ 次。这会导致 $O(\frac{\log N}{\log N-\log M})$ 的速度提升，可能会高出一个数量级。

在实际应用中，由于递归本身的开销，完全使用递归可能并不是最优解。因此，混合算法的出现，即在迭代到一定深度后，切换到递归方式，这种方法综合了递归的优点和迭代高效的优点，能在实际应用中取得更好的效果。

动态规划

类似的推理可以应用于动态规划算法的实现，但会得到相反的结果。我们来考虑一个经典的背包问题（knapsack problem）：给定 $N$ 个物品，它们都有正整数的成本 $c_i$ ，选择一组物品，使得总成本不超过给定的常数 $W$ ，且总成本是最大的。

解决这个问题的方法是引入状态 $f[n,w]$ ，表示的是我们只使用前 $n$ 个物品，并且总成本不超过 $w$ 时能获得的最大总成本。为了计算这个状态值，我们会考虑两种可能的情况：拿取第 $n$ 个物品，或者不拿。根据动态规划的逻辑，我们总是做出这样的决策：在保证总成本不超过 $w$ 的前提下，尽可能让总成本达到最大。通过这种方式，我们可以在常数时间 $O(1)$ 内算出每一个状态 $f[n,w]$ 的值。

Python有一个方便的lru_cache装饰器，可以用于实现带有备忘录（Memoization）的递归：

@lru_cache
def f(n, w):
    # check if we have no items to choose
    if n == 0:
        return 0
    
    # check if we can't pick the last item (note zero-based indexing)
    if c[n - 1] > w:
        return f(n - 1, w)
    
    # otherwise, we can either pick the last item or not
    return max(f(n - 1, w), c[n - 1] + f(n - 1, w - c[n - 1]))

在计算 $f[N,W]$ 时，递归可能会遍历所有可能的 $N$ 和 $W$ 的组合，访问多达 $O(N⋅W)$ 个不同的状态，这在理论上是高效的，但在实际中却相当慢。即使消除了Python递归本身的开销和LRU缓存所做的哈希表查询的开销，由于在执行过程中大部分时间都在进行随机I/O，所以仍然会非常慢。

替代方案就是创建一个用于动态规划的二维数组，并用一个嵌套循环来代替递归，就像这样：

int f[N + 1][W + 1] = {0}; // this zero-fills the array

for (int n = 1; n <= N; n++)
    for (int w = 0; w <= W; w++)
        f[n][w] = c[n - 1] > w ?
                  f[n - 1][w] :
                  max(f[n - 1][k], c[n - 1] + f[n - 1][w - c[n - 1]]);

注意我们只用到了动态规划过程中的前一层数据来计算下一层。这意味着，如果缓存中能够存储一层数据，我们只需往外部存储器中写入 $O(\frac{N⋅W}{B})$ 个数据块。

更进一步，如果我们只关心答案而不是整个过程，其实我们并不需要存储整个二维数组，而只需要存储最后一层。只需维护一个含 $W$ 个值的数组，我们就能用 $O(W)$ 的内存完成任务。为了简化代码，我们可以稍微修改动态规划的方式，即存储一个二进制值来表示是否可以通过已经被考虑过的物品得到恰好为 $w$ 的和。这种方法的运算速度较快，因为只需要进行逻辑运算，而非数值运算。

bool f[W + 1] = {0};
f[0] = 1;
for (int n = 0; n < N; n++)
    for (int x = W - c[n]; x >= 0; x--)
        f[x + c[n]] |= f[x];

顺带说一句，上述代码只使用简单的位操作，可以通过使用位集bitset进行进一步优化。

std::bitset<W + 1> b;
b[0] = 1;
for (int n = 0; n < N; n++)
    b |= b << c[n];

不可思议的是，上述代码仍然有一些改进的空间，我们稍后再讨论这个问题。

稀疏表

稀疏表（Sparse Table）是一种静态数据结构，常用于解决静态RMQ（Range Minimum/Maximum Query，区间最小/大值查询）问题，以及任何类似的幂等范围归约（idempotent range reductions）计算。可以被正式定义为一个 $\log n×n$ 大小的二维数组：

$t[k][i] = \min\{a_i, a_{i+1}, \dots,a_{i+2^k-1}\}$

通俗地说: 我们储存每一个长度为2的幂次的段落中的最小值。

这个二维数组可以在常数时间内计算任意段落的最小值，因为对于任意段落，我们总是可以将其分解为两个可能重叠的子段落，子段落的大小也是2的幂次（因此两个子段落的最小值通过查表可知），两个子段落的并集就是整个段落。

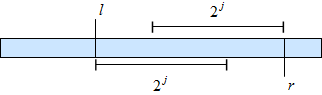
因此我们只需要取这两个最小值中较小的那个，即为所求区间的最小值：

int rmq(int l, int r) { // half-interval [l; r)
    int t = __lg(r - l);
    return min(mn[t][l], mn[t][r - (1 << t)]);
}

__lg函数是GCC中可用的内置函数，用于计算一个数的二进制对数并向下取整。在内部，它使用clz（count leading zeros，统计二级制表示中高位零的个数）指令，并从32（在32位整数的情况下）中减去这个计数（从而得到最高位1的位置，即二进制对数向下取整），因此只需要几个周期，运算速度很快。

我在这篇文章中提起稀疏表的原因是构建它的方式有很多种，这些方法在内存操作的效率上会有所不同。通常，我们可以通过动态规划的方式，按照 $i$ 或 $k$ 递增的顺序进行迭代，在 $O(n\log n)$ 的时间复杂度内构建稀疏表。这会用到下面的公式：

$t[k][i]=\min (t[k−1][i],t[k−1][i+2^{k−1}])$

现在，有两个设计选择要做：首先对数大小 $k$ 应该是第一个维度还是第二个维度，以及应该先迭代 $k$ 还是再迭代 $i$ 。这意味着有 $2×2=4$ 种构建方法，下面是最优选择：

int mn[logn][maxn];

memcpy(mn[0], a, sizeof a);

for (int l = 0; l < logn - 1; l++)
    for (int i = 0; i + (2 << l) <= n; i++)
        mn[l + 1][i] = min(mn[l][i], mn[l][i + (1 << l)]);

这种内存布局和迭代顺序的组合，是唯一一种以优美的线性过程生成结果，工作效率是其他方法的大约3倍。作为一个练习，思考一下其他三种变体，想想为什么它们运行得更慢。

结构数组与数组结构

假设你想实现一个二叉树，并将其字段存储在不同的数组中：

int left_child[maxn], right_child[maxn], key[maxn], size[maxn];

这种存储布局，即我们将每个字段与其他字段分开存储的方式，被称为数组结构（struct-of-arrays，SoA）。在大多数情况下，对树进行操作时，你会访问一个节点，然后立即访问其内部的所有或大部分数据。如果这些字段分开存储，那么就意味着它们也位于不同的内存块中。如果请求的字段只有部分已经被缓存，那么你仍然需要等待最慢的那个被取出。

相比之下，如果将其存储为结构数组（array-of-structs，AoS），你只需要读取少大约4倍的块就可以获取所有数据，因为一个节点的所有数据都存储在同一个块中，并且一次性取出。

struct Node {
    int left_child, right_child, key, size;
};

Node t[maxn];

AoS布局通常更适合于数据结构，但是SoA依然有很大的用途：虽然在查找方面性能较差，但在线性扫描上却更有优势。

这种设计差异在数据处理应用中非常重要。例如，数据库可以是行主序存储（row-oriented）或列主序存储（column-oriented，也叫columnar）：

行主序存储格式用于需要在大型数据集中查询有限数量的对象以及获取它们所有或大部分字段的情况。例如：PostgreSQL，MongoDB。
列主序存储格式用于大数据的处理和分析，例如需要扫描所有内容以计算某些统计量。例如：ClickHouse，Hbase。

列主序存储格式还有额外的优点，就是你可以只读取你需要的字段，因为不同的字段保存在单独的外部内存区域。