列表排名

在这一部分，我们将应用外部排序和连接来解决一个表面上看起来无用但实际上在大量外部存储和并行算法中被广泛使用的关键原语问题。

问题：给定一个单向链表，计算每个元素的排名（rank），等于其到最后一个元素的距离。下面是列表排名问题的输入和输出示例：

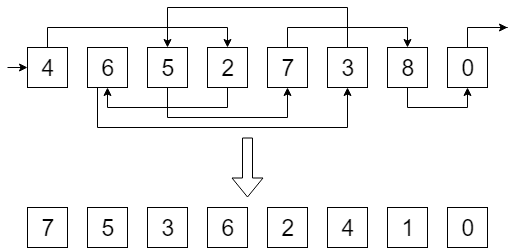
这个问题在 RAM 模型中可以轻易地解决：你只需要遍历整个列表并进行计数。但是，在外部存储器环境中直接使用指针跳跃的方式可能并不能很好地工作，因为列表节点是随机存储的，在最坏的情况下，读取每个新节点都可能需要读取一个新的块。

算法

考虑关于这个问题的一个更加通用的版本。现在，每个元素都有一个权重 $w_i$ ，对于每个元素，需要计算的不再是它之前的元素数量（即它的排名），而是需要计算它之前所有元素的权重之和。如果希望退化到最初的问题（即每个元素之前的元素数量），可以简单地将每个元素的权重都设为1，这样元素权重之和就等同于元素数量。

该算法的主要思想是删除一些元素（或者元素的一部分），用递归的方式来求解这个减小规模的问题。解决之后，算法会根据这些权重排名结果来重建初始问题的答案。

考虑三个连续的元素 $x$ ， $y$ 和 $z$ 。假设我们删除了 $y$ ，然后针对包含剩余元素 $x$ 和 $z$ 的列表计算答案，现在我们尝试重建原始三元素列表的答案。在这个过程中，元素 $x$ 的权重是正确的，不需要修改。问题的关键在于如何计算已删除元素 $y$ 的答案，并根据 $y$ 的答案来调整 $z$ 的答案。具体来说：

${w_y}^, = w_y + w_x$
${w_z}^, = w_z + w_y + w_z$

现在，我们可以删除第一个元素，把问题简化为更小规模的子问题来递归求解，然后再用这些解来构造原问题的解。但是在更新子问题的解时，需要考虑到原数组中元素的相邻关系，而由于内存限制可能无法同时保存所有的数组元素，所以需要每次都要去扫描整个数组以确定相邻元素的位置，这会导致算法的时间复杂度为 $O(n^2)$ 。

对于每一步，在满足算法规则的前提下，为了提高效率，我们的目标通常是尽可能多地移除元素。然而，这个算法有一个约束条件：不能移除两个连续的元素。若违反这一约束条件，那么后续需要合并各子问题的解以得出最终结果的过程就会变得复杂。

理想情况下，我们想将我们的列表分成偶数元素和奇数元素，但这样做并不比最初的问题更简单。一个变通的方法是随机选择元素：为每个元素扔一枚硬币，然后移除所有“正面”后面紧跟着的那一个“反面”。这样就永远不会选中两个连续的元素，平均而言我们减少了当前列表的1/4。这个解决方案的算术复杂度仍然是线性的，因为

$T(N) = T(\frac{3}{4}N) = O(N)$

这里唯一棘手的部分是如何在外部存储中实现合并步骤。为了高效地进行操作，我们需要以以下形式维护我们的列表：

一个元组列表 $(i,j)$ ，表示元素 $j$ 在元素 $i$ 之后。
一个元组列表 $(i, w_i)$ ，表示元素 $i$ 当前的权重为 $w_i$ 。
一个已删除元素的列表。

现在，在随机删除了部分元素，递归地解决了更小规模的问题之后，为了恢复答案，我们需要使用三个指针遍历所有列表来寻找被删除的元素。对于每一个这样的元素，我们将 $(j,w_i)$ 写入一个独立的表格，这表示在递归步骤之前我们需要将 $w_i$ 加到 $j$ 上。然后我们可以将这个新表与初始权重表连接（join），将这些额外的权重加到它们之上。