现代硬件算法[8.4]: 外部排序

外部排序

现在，让我们试着为新的外部存储模型设计一些实际有用的算法。我们在这个部分的目标是慢慢构建更复杂的东西，最终达到外部排序及其有趣的应用。

这个算法将基于标准的归并排序算法，所以我们首先需要推导出它的主要原始形式。

归并

问题：给定两个有序数组$a$（长度为$N$）和$b$（长度为$M$），要生成一个包含两者所有元素的有序数组$c$（长度为$N+M$）。

用于合并排序数组的标准的双指针技巧如下所示：

void merge(int *a, int *b, int *c, int n, int m) {
    int i = 0, j = 0;
    for (int k = 0; k < n + m; k++) {
        if (i < n && (j == m || a[i] < b[j]))
            c[k] = a[i++];
        else
            c[k] = b[j++];
    }
}

在内存操作方面，我们只需线性地读取$a$和$b$的所有元素并线性地将所有元素写入$c$。由于这些读取和写入操作可以被缓存，所以它需要 $SCAN(N+M) $ 次 I/O 操作来完成。

到目前为止所展示的例子都相对简单，不管是在计算理论还是实际操作上，它们和RAM模型的分析并无太大区别，只是在最后结果中有一步除以块大小$B$的操作。但这个规则在下面这总情况下并不适用：

k路归并：

考虑稍微复杂一些的情况，需要合并的不只是两个数组，而是总大小为N的k个数组 - 同样地，操作过程是查看每个数组的第一个元素（k个值），选择其中的最小值，并将这个最小值写入输出数组c，最后，将指向该最小值的迭代器（即指针或者索引）向前移动一步。

在标准的 RAM 模型中，渐近复杂性会被乘上$k$，因为我们需要执行 $O(k)$ 次比较来填充每一个元素。但在外部存储器模型中，存储在内存中的操作是“免费”的，不对总体的时间复杂性产生影响。因此，只要我们能够在内存中装下$(k+1)$个完整的块，不论我们怎么操作这些数据，总体的时间复杂性都不会受到影响。也就是说，$k = O(\frac{M}{B})$（这里$M$为内存总量，$B$为块大小，这里想表达的是只要$k$不大于 $M/B$（内存最多容纳块数），那么整体的渐近复杂性就不会发生改变）。

还记得我们在介绍计算模型是提到的$M \gg B$的假设吗？如果对于任意 $\epsilon > 0$ 有 $M ≥ B^{1+\epsilon}$，也就是说如果内存足够大，足以装下一个高于B的任意幂次的块，这当然包括$O(\frac{M}{B})$。这种情况被称为高缓存假设，这在许多其他外部存储器算法中也是需要的。

归并排序

标准的归并排序算法的正常复杂度为$O(N\log_2N)$：在算法的每一层操作中（每次将问题规模缩小一半，所以有$O(\log_2N)$层），需要遍历$N$个元素，并在线性时间内将它们合并。

在外部存储模型中，当我们读取一个大小为$M$的块时，我们可以“免费”对其元素进行排序，因为它们已经在内存中。这样我们可以将数组分割为$O(\frac{N}{M})$个连续元素的块，并分别对它们进行排序作为基础步骤，然后再合并它们。

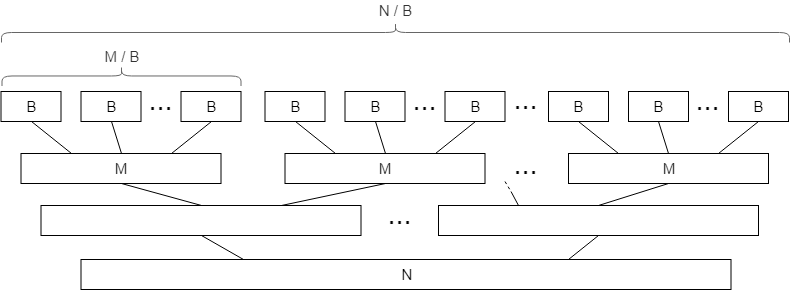
这实际上意味着，就I/O操作而言，前$O(\log M)$层的归并排序是“免费”的，总共有$O(\log_2\frac{N}{M})$层非零成本层，每层需要做总共 $O(\frac{N}{B})$ IOPS 来合并。这使得总的I/O复杂度为：

$$O(\frac{N}{B}\log_2\frac{N}{M})$$

这是相当快的过程。如果我们有1GB的内存和10GB的数据，这基本上意味着我们在排序这些数据时，所需的努力比仅读取数据（$O(⌈\frac{N}{B}⌉$)）要多三点几倍（$\log_210$）。然而，有趣的是我们实际上可以做得更好。

k路归并排序

在上面的讨论中，我们了解到在外部存储模型中，我们可以像合并两个数组一样轻松地合并k个数组，代价就是我们必须读取所有这些数组的数据。那么，我们为什么不将这一方法应用到归并排序中呢？

我们将和以前一样对内存中每个大小为$M$的块进行排序，但是在合并阶段，我们不只将两个排序后的块进行合并，而且还会取尽可能多的块，选择适应我们内存大小的k路合并。这样，合并树的高度将大大降低，而每层仍然会在 $O(\frac{N}{B})$ IOPS内完成。

我们一次可以合并多少个已排序数组？答案是$k=\frac{M}{B}$，因为我们需要为每个数组分配一个内存块。由于合并总层数将减少为$\log_{\frac{M}{B}}\frac{N}{M}$，因此总的复杂度将减少为：

$$SORT(N) \stackrel{def}= O(\frac{N}{B}\log_{\frac{M}{B}}\frac{N}{M})$$

在我们的例子中，我们有10GB的数据，1GB的内存，硬盘驱动器的块大小大约为1MB。这使得$\frac{M}{B}=1000$, $\frac{N}{M}=10$，所以对数值小于一（即$log_{1000}10=\frac{1}{3}$）。当然，我们对数组进行排序不可能比读取它更快，所以这种分析适用于我们有非常大的数据集，小内存和/或较大的块大小的情况，这在现实中比较少见。

具体实现

在更现实的约束条件下，我们不会选择用$\log_{\frac{M}{B}}\frac{N}{M}$层，而是只使用两个步骤来操作数据：第一步在包含M个元素的块中排序数据，第二步是一次性合并所有这些块。从I/O操作的观点来看，这样做我们只需遍历两次数据集。对于1GB的RAM和1MB的块大小，这种方式可以对高达1TB的数组进行排序。

下面是用C++实现的第一步操作。这个程序打开一个大小为若干GB的包含未排序整数的二进制文件，以256MB的块读取它们，将它们在内存中排序，然后将它们写回名为part-000.bin，part-001.bin，part-002.bin等的文件中:

const int B = (1<<20) / 4; // 1 MB blocks of integers
const int M = (1<<28) / 4; // available memory

FILE *input = fopen("input.bin", "rb");
std::vector<FILE*> parts;

while (true) {
    static int part[M]; // better delete it right after
    int n = fread(part, 4, M, input);

    if (n == 0)
        break;
    
    // sort a block in-memory
    std::sort(part, part + n);
    
    char fpart[sizeof "part-999.bin"];
    sprintf(fpart, "part-%03d.bin", parts.size());

    printf("Writing %d elements into %s...\n", n, fpart);

    FILE *file = fopen(fpart, "wb");
    fwrite(part, 4, n, file);
    fclose(file);
    
    file = fopen(fpart, "rb");
    parts.push_back(file);
}

fclose(input);

现在剩下的就是将它们合并在一起。现代硬盘的带宽可能相当高，并且需要合并的部分可能很多，因此，这个阶段的I/O效率并不是我们唯一关心的问题：我们还需要找到一种合并$k$个数组的方法，比通过$O(k)$次比较找到最小值的方法更快。如果我们维护这$k$个元素的一个最小堆，那么对每个元素而言，我们可以在$O(\log k)$时间内完成这个任务，这与堆排序几乎一样。

下面就是如何实现它。首先，我们需要一个堆（C++中的priority_queue）：

struct Pointer {
    int key, part; // the element itself and the number of its part

    bool operator<(const Pointer& other) const {
        return key > other.key; // std::priority_queue is a max-heap by default
    }
};

std::priority_queue<Pointer> q;

然后，我们需要分配并填充buffer：

const int nparts = parts.size();

auto buffers = new int[nparts][B]; // buffers for each part
int *l = new int[nparts],          // # of already processed buffer elements
    *r = new int[nparts];          // buffer size (in case it isn't full)

// now we add fill the buffer for each part and add their elements to the heap
for (int part = 0; part < nparts; part++) {
    l[part] = 1; // if the element is in the heap, we also consider it "processed"
    r[part] = fread(buffers[part], 4, B, parts[part]);
    q.push({buffers[part][0], part});
}

我们现在只需要将堆中的元素取出并放入结果文件中，直到堆为空，并且做到谨慎地批量写入和读取元素：

FILE *output = fopen("output.bin", "w");

int outbuffer[B]; // the output buffer
int buffered = 0; // number of elements in it

while (!q.empty()) {
    auto [key, part] = q.top();
    q.pop();

    // write the minimum to the output buffer
    outbuffer[buffered++] = key;
    // check if it needs to be committed to the file
    if (buffered == B) {
        fwrite(outbuffer, 4, B, output);
        buffered = 0;
    }

    // fetch a new block of that part if needed
    if (l[part] == r[part]) {
        r[part] = fread(buffers[part], 4, B, parts[part]);
        l[part] = 0;
    }

    // read a new element from that part unless we've already processed all of it
    if (l[part] < r[part]) {
        q.push({buffers[part][l[part]], part});
        l[part]++;
    }
}

// write what's left of the output buffer
fwrite(outbuffer, 4, buffered, output);

//clean up
delete[] buffers;
for (FILE *file : parts)
    fclose(file);
fclose(output);

这个实现方法在性能上并不十分高效，看起来也不够安全（基本上是纯C语言实现），但是是一个帮助我们理解和使用低级内存API的很好教育示例。

连接

排序的主要应用不是单独使用，而是作为其他操作的中间步骤。外部排序的一个重要实际应用就是连接（joining，如SQL中的join），会在数据库和其他数据处理应用中使用。

**问题：**给定两个分别包含元组$(x_i,a_{x_i})$和元组$(y_i,b_{y_i})$的列表，输出一个列表$(k,a_{x_k},b_{y_k})$使得$x_k = y_k$。

最优解是对两个列表进行排序，然后使用标准的双指针技术来合并它们。在这里，I/O的复杂度与排序相同，如果数组已经排序，那么复杂度为$O(\frac{N}{B})$。这就是为什么大多数数据处理应用（数据库，MapReduce系统）都希望保持他们的数据至少是部分有序的。

**其他方法：**注意，这种分析仅适用于外部存储设置——也就是说，如果你没有足够的内存去读取整个数据集，该方法才适用。在现实世界中，可能有更快的备选方法。

其中最简单的可能就是哈希连接（hash join），其大致过程如下：

def join(a, b):
    d = dict(a)
    for x, y in b:
        if x in d:
            yield d[x]

在外部存储中，使用哈希表来连接两个列表是不可行的，因为即使每个元素都只存在于其中一个列表中，也会涉及到$O(M)$次块读取。

另一种方法是使用其他排序算法，如基数排序（radix sort）。特别是，如果有足够的内存来维护所有可能的键值的缓冲区，基数排序将需要$O(\frac{N}{B}⋅w)$次块读取（其中 $w$ 是键值的位数），这在处理小键值和大数据范围时，可能会更快。