前言

主要针对CPU后端，基于/source/backend/cpu/compute/Convolution1x1Strassen.cpp源码展开。

以输入大小：1 x 8 x 224 x 224（C4 Pack为1 x 2 x 224 x 224 (x 4)），权重大小: 16 x 8 x 1 x 1(MNN中将其变换为1 x 4 x 8 (x 4)，即对输出通道（卷积核个数）进行C4 Pack), 输出1 x 16 x 224 x 224（C4 Pack为1 x 4 x 224 x 224 (x 4)）为例进行辅助说明。

没有特殊说明，代码版本均为MNN release_1.2.3版本

适用条件

bool fastWay = common->kernelY() == 1 && common->kernelX() == 1
        && output->width() == input->width() && output->height() == input->height()
        && common->strideX() == 1 && common->strideY() == 1;
if (fastWay) {
    return new Convolution1x1Strassen(common, backend, originWeight, originWeightSize, bias, biasSize);
}

可见只针对kernelX = kernelY = strideX = strideY = 1的卷积操作。

权重重排

初始权重为NCHW排布：16 x 8 x 1 x1，按NC/4HW4重排后为 1x 4 x 8 (x 4)。即针对卷积核个数进行C4 Pack，示意图如下：

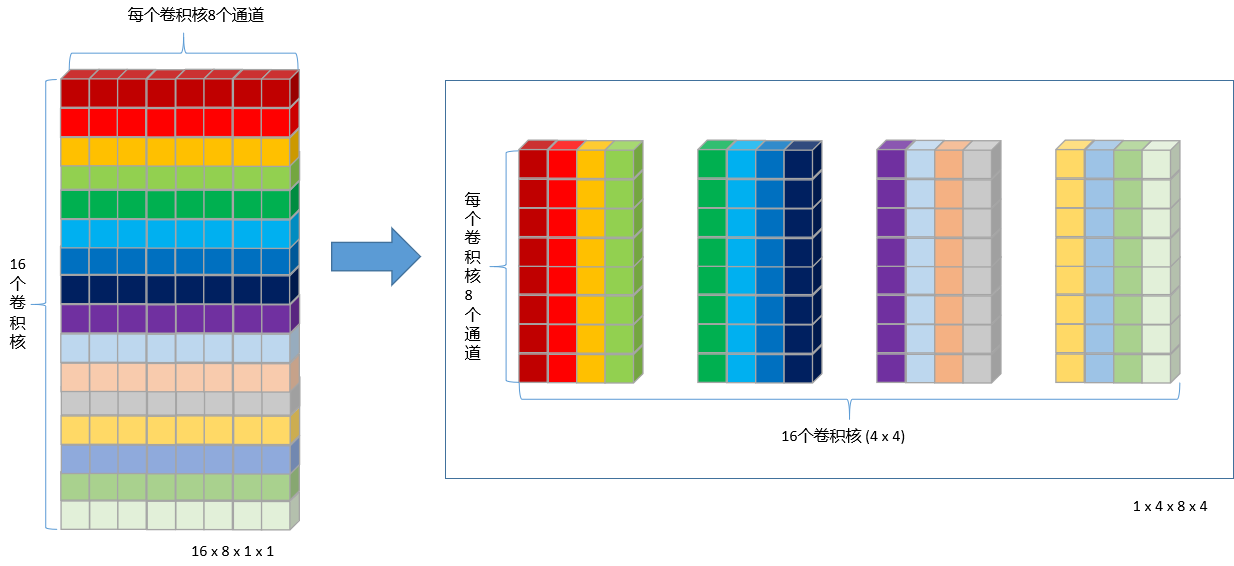
执行代码段如下：

core->MNNPackForMatMul_B(mResource->mWeight->host<float>(), originWeight, outputCount, mSrcCount, true);

onResize

Strassen的所有步骤实现不在onExecute里，onExecute中只通过mFunctions中的函数指针调用onResize中的实现（将计算步骤拆解成若干个lambda函数，放到mFunctions中）。

MNN多线程加速在这里有不同的选择，当featureMap尺寸很大时，根据featureMap进行划分，每个线程处理一块，否则根据输出通道划分，每个线程处理一个（C4）通道：

if (matrixSizeE > CONVOLUTION_TILED_NUMBER * 8 * numberThread && matrixSizeE > ocC4) {
    // Divide in plane, in this case the divide equal numberThread
    ...	
}else {
    // Divide in ocC4
    ...
}

暂时按照单线程进行说明。创建StrassenMatMulComputer类对象，通过onEncode接口进入StrassenMatMulComputer实现类：

unit.mStracssenComputor.reset(new StrassenMatrixComputor(backend(), false, maxDepth));
...
auto code = unit.mStracssenComputor->onEncode(mTempInputVector, mTempOutputVector, postParameters, ic, oc);

注意这里StrassenMatMulComputer类构造函数的第二个参数为false，即mSupportMultiThread=false，表示再往下的操作不会再进行线程划分，因为上面已经做过了。

onEncode会调用_generateMatMul，其中包含Strassen分块的主要实现。

_generateMatMul

Strassen算法本身包含矩阵分块的递归计算，因此_generateMatMul是个递归函数。

那么先看递归的终止条件，即何时结束分块操作，进行普通的卷积运算。终止条件有两个：

1. 嵌套深度超过设定的最大深度时，或者 $A$ 和 $B$ 矩阵不能再继续分块时：

if (currentDepth >= mMaxDepth || eSub == 0 || hSub == 0 || l % (2 * core->pack) != 0 || l % (2 * lP) || l % (2 * packHUnit) != 0) {
    return _generateBasicMatMul(e, l, h, AT, BT, CT, COT, postParameters);
}

1. 读写内存的次数大于普通卷积实现时：

if (saveCost <= 0.0f) {
    return _generateBasicMatMul(e, l, h, AT, BT, CT, COT, postParameters);
}

递归部分代码的运算顺序和内存buffer使用情况与上一篇介绍的改进版本Strassen算法是一致的，通过将分块操作分解成若干个lambda函数，压入mFunctions向量，在onExecute时执行。

// Strassen Construct
auto bn = backend();
auto allocator = static_cast<CPUBackend*>(backend())->getBufferAllocator();
currentDepth += 1;
auto maxlH = std::max(lSub, hSub);
AutoMemory YAddr(hSub * lSub * core->bytes, allocator);
AutoMemory XAddr(maxlH * eSub * core->bytes, allocator);
if (nullptr == XAddr.get().first || nullptr == YAddr.get().first) {
    return OUT_OF_MEMORY;
}
MatrixInfo Y;
Y.stackIndex = (int)mStack.size();
mStack.emplace_back((uint8_t*)YAddr.get().first + YAddr.get().second);
Y.offsetBytes = 0;
Y.lineStrideBytes = lSub * core->bytes * hP;
MatrixInfo X;
X.stackIndex = (int)mStack.size();
X.offsetBytes = 0;
X.lineStrideBytes = eSub * core->bytes * core->pack;
mStack.emplace_back((uint8_t*)XAddr.get().first + XAddr.get().second);

MatrixInfo CX;
CX.stackIndex = X.stackIndex;
CX.offsetBytes = 0;
CX.lineStrideBytes = eSub * core->bytes * core->pack;

MatrixInfo a11 = AT;
MatrixInfo a12 = AT;
a12.offsetBytes = AT.offsetBytes + AT.lineStrideBytes * lSubUnit;
MatrixInfo a21 = AT;
a21.offsetBytes = AT.offsetBytes + eSub * core->pack * core->bytes;
MatrixInfo a22 = AT;
a22.offsetBytes = AT.offsetBytes + eSub * core->pack * core->bytes + AT.lineStrideBytes * lSubUnit;

MatrixInfo b11 = BT;
MatrixInfo b12 = BT;
b12.offsetBytes = BT.offsetBytes + BT.lineStrideBytes * (hSub / hP);
MatrixInfo b21 = BT;
b21.offsetBytes = BT.offsetBytes + lSub * hP * core->bytes;
MatrixInfo b22 = BT;
b22.offsetBytes = BT.offsetBytes + BT.lineStrideBytes * (hSub / hP) + lSub * hP * core->bytes;

MatrixInfo c11 = CT;
MatrixInfo c12 = CT;
c12.offsetBytes = CT.offsetBytes + CT.lineStrideBytes * (hSub / core->pack);
MatrixInfo c21 = CT;
c21.offsetBytes = CT.offsetBytes + eSub * core->pack * core->bytes;
MatrixInfo c22 = CT;
c22.offsetBytes = CT.offsetBytes + eSub * core->pack * core->bytes + CT.lineStrideBytes * (hSub / core->pack);

MatrixInfo Empty;
Empty.stackIndex = -1;

{
    // S3=A11-A21, T3=B22-B12, P7=S3*T3
    auto f = [a11, a21, b22, b12, X, Y, eSub, lSub, hSub, numberThread, core, hP, this, bWidth, aHeight, bHeight](int tId) {
        auto xAddr = mStack[X.stackIndex] + X.offsetBytes;
        auto yAddr = mStack[Y.stackIndex] + Y.offsetBytes;
        auto a11Ptr = mStack[a11.stackIndex] + a11.offsetBytes;
        auto a21Ptr = mStack[a21.stackIndex] + a21.offsetBytes;
        MNNMATRIX_SUB_MULTITHREAD(xAddr, a11Ptr, a21Ptr, eSub, X.lineStrideBytes, a11.lineStrideBytes, a21.lineStrideBytes, aHeight, core);
        MNNMATRIX_SUB_MULTITHREAD(yAddr, mStack[b22.stackIndex] + b22.offsetBytes, mStack[b12.stackIndex] + b12.offsetBytes, bWidth, Y.lineStrideBytes, b22.lineStrideBytes, b12.lineStrideBytes, bHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f, numberThread));
    auto code = _generateMatMul(eSub, lSub, hSub, X, Y, c21, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
}
{
    // S1=A21+A22, T1=B12-B11, P5=S1T1
    auto f = [a22, a21, b11, b12, X, Y, eSub, lSub, hSub, numberThread, hP, core, this, bWidth, aHeight, bHeight](int tId) {
        MNNMATRIX_ADD_MULTITHREAD(mStack[X.stackIndex] + X.offsetBytes, mStack[a21.stackIndex] + a21.offsetBytes, mStack[a22.stackIndex] + a22.offsetBytes , eSub, X.lineStrideBytes, a21.lineStrideBytes, a22.lineStrideBytes, aHeight, core);
        MNNMATRIX_SUB_MULTITHREAD(mStack[Y.stackIndex] + Y.offsetBytes, mStack[b12.stackIndex] + b12.offsetBytes, mStack[b11.stackIndex] + b11.offsetBytes, bWidth, Y.lineStrideBytes, b12.lineStrideBytes, b11.lineStrideBytes, bHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f, numberThread));
    auto code = _generateMatMul(eSub, lSub, hSub, X, Y, c22, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
}
{
    // S2=S1-A11, T2=B22-T1, P6=S2T2
    auto f = [a11, b22, X, Y, eSub, lSub, hSub, numberThread, hP, core, this, bWidth, aHeight, bHeight](int tId) {
        auto xAddr = mStack[X.stackIndex] + X.offsetBytes;
        auto yAddr = mStack[Y.stackIndex] + Y.offsetBytes;
        MNNMATRIX_SUB_MULTITHREAD(xAddr, xAddr, mStack[a11.stackIndex] + a11.offsetBytes, eSub, X.lineStrideBytes, X.lineStrideBytes, a11.lineStrideBytes, aHeight, core);
        MNNMATRIX_SUB_MULTITHREAD(yAddr, mStack[b22.stackIndex] + b22.offsetBytes, yAddr, bWidth, Y.lineStrideBytes, b22.lineStrideBytes, Y.lineStrideBytes, bHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f, numberThread));
    auto code = _generateMatMul(eSub, lSub, hSub, X, Y, c12, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
}
{
    // S4=A12-S2, P3=S4*B22, P1=A11*B11
    auto f = [a12, X, eSub, aHeight, numberThread, core, this](int tId) {
        auto xAddr = mStack[X.stackIndex] + X.offsetBytes;
        MNNMATRIX_SUB_MULTITHREAD(xAddr, mStack[a12.stackIndex] + a12.offsetBytes, xAddr, eSub, X.lineStrideBytes, a12.lineStrideBytes, X.lineStrideBytes, aHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f, numberThread));
    auto code = _generateMatMul(eSub, lSub, hSub, X, b22, c11, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
    code = _generateMatMul(eSub, lSub, hSub, a11, b11, CX, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
}
{
    // U2=P1+P6, U3=U2+P7, U4=U2+P5, U7=U3+P5
    // U5=U4+P3, T4=T2-B21, P4=A22*T4
    auto f = [c11, c12, c21, c22, b21, X, Y, eSub, bWidth, cHeight, bHeight, numberThread, core, this](int tId) {
        for (int y = tId; y < cHeight; y+=numberThread) {
            core->MNNStrassenMergeCFunction((float*)(mStack[c11.stackIndex] + c11.offsetBytes + y * c11.lineStrideBytes), (float*)(mStack[c12.stackIndex] + c12.offsetBytes + y * c12.lineStrideBytes), (float*)(mStack[c21.stackIndex] + c21.offsetBytes + y * c21.lineStrideBytes), (float*)(mStack[c22.stackIndex] + c22.offsetBytes + y * c22.lineStrideBytes), (float*)(mStack[X.stackIndex] + X.offsetBytes + y * X.lineStrideBytes), 0, eSub, 1);
        }
        auto yAddr = mStack[Y.stackIndex] + Y.offsetBytes;
        MNNMATRIX_SUB_MULTITHREAD(yAddr, yAddr, mStack[b21.stackIndex] + b21.offsetBytes, bWidth, Y.lineStrideBytes, Y.lineStrideBytes, b21.lineStrideBytes, bHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f, numberThread));
    auto code = _generateMatMul(eSub, lSub, hSub, a22, Y, c11, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
}
{
    // U6=U3-P4, P2=A12*B21, U1=P1+P2
    auto f0 = [c11, c21, eSub, cHeight, numberThread, core, this](int tId) {
        auto cw = eSub;
        auto c21Addr = mStack[c21.stackIndex] + c21.offsetBytes;
        MNNMATRIX_SUB_MULTITHREAD(c21Addr, c21Addr, mStack[c11.stackIndex] + c11.offsetBytes, cw, c21.lineStrideBytes, c21.lineStrideBytes, c11.lineStrideBytes, cHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f0, numberThread));
    auto code = _generateMatMul(eSub, lSub, hSub, a12, b21, c11, Empty, currentDepth, {});
    if (code != NO_ERROR) {
        return code;
    }
    auto f1 = [c11, X, eSub, cHeight, numberThread, core, this](int tId) {
        auto cw = eSub;
        auto c11Ptr = mStack[c11.stackIndex] + c11.offsetBytes;
        auto xAddr = mStack[X.stackIndex] + X.offsetBytes;
        MNNMATRIX_ADD_MULTITHREAD(c11Ptr, c11Ptr, xAddr, cw, c11.lineStrideBytes, c11.lineStrideBytes, X.lineStrideBytes, cHeight, core);
    };
    mFunctions.emplace_back(std::make_pair(f1, numberThread));
	... // post 
}

下面着重看下1 x 1卷积的矩阵乘法和分块逻辑：

普通的`1 × 1`卷积的矩阵乘法（ $C=AB$ ）：

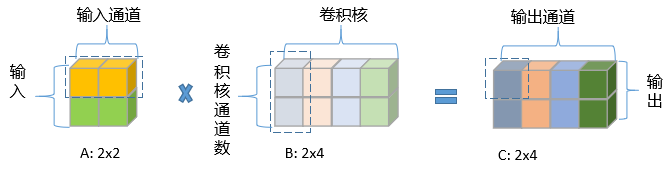
蓝色虚线框代表一次卷积乘加运算

MNN`C4 Pack`的`1 × 1`卷积的矩阵乘法：

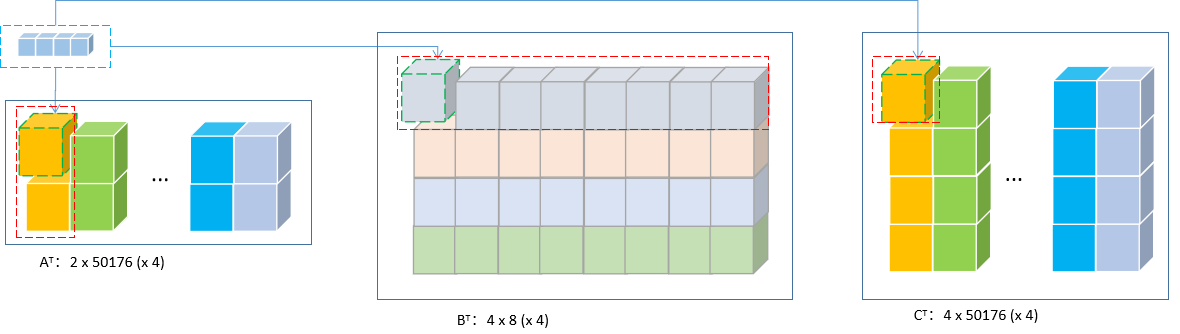
上图中每个方块代表一个C4 Pack，输入按输入通道pack，卷积核按卷积核个数pack，输出按输出通道pack;
输入2 x 224 x 224 (x 4)可以看作普通矩阵乘法中 $A$ 的转置（2 x 50176 (x 4)），卷积核4 x 8 (x4)可以看作普通矩阵乘法中 $B$ 的转置，输出4 x 224 x 224 (x 4)可以看作普通矩阵乘法中 $C$ 的转置（4 x 50176 (x 4)）。
如果当前矩阵不再进行分块，则一次卷积乘加运算对应为红色虚线框中的元素，直观可以理解为 $C^T=(AB)^T=B^TA^T$ ，实际的MNN执行中，会先对 $A$ 矩阵进行重排（MNNPackC4ForMatMul_A），具体下文再谈。

Strassen矩阵分块：

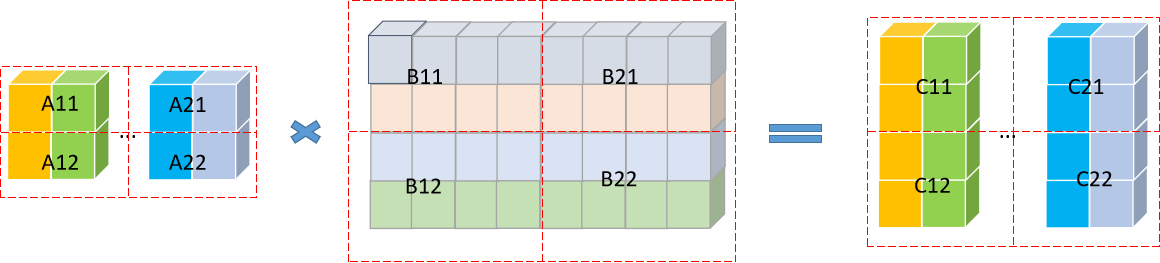
在转置形式下进行分块运算，各子块的矩阵乘法递归调用_generateMatMul直到满足递归终止条件后，切换到普通矩阵乘法。

_generateBasicMatMul

_generateBasicMatMul函数中会调用_generateTrivalMatMul执行普通1 x 1卷积操作，核心代码如下：

mFunctions.emplace_back(
    std::make_pair([cStride, l, h, xCount, AT, BT, CT, COT, tileHostOrigin, unitNumber, bExtraStride, numberThread, eReal, eP, active, this](int tId) {
        auto core = static_cast<CPUBackend*>(backend())->functions();
        size_t parameters[6];
        parameters[0] = xCount * core->bytes;
        parameters[1] = l;
        parameters[2] = h;
        parameters[3] = cStride;
        parameters[4] = 0;
        parameters[5] = bExtraStride;
        auto tileHost = tileHostOrigin + eP * parameters[1] * tId * core->bytes;
        const float* postParametersPtr = nullptr;
        if (!active.empty()) {
            postParametersPtr = active.data();
        }
        auto aHost = mStack[AT.stackIndex] + AT.offsetBytes;
        auto bHost = mStack[BT.stackIndex] + BT.offsetBytes;
        auto cHost = mStack[CT.stackIndex] + CT.offsetBytes;
        const uint8_t* biasPtr = nullptr;
        if (-1 != COT.stackIndex) {
            biasPtr = mStack[COT.stackIndex] + COT.offsetBytes;
        }
        auto packUnit = core->bytes * core->pack;
        int32_t info[4];
        int32_t stride[4];
        stride[0] = eP;
        stride[1] = parameters[1];
        stride[2] = 0;
        stride[3] = 0;
        info[0] = 1;
        info[1] = eReal;
        info[2] = eP;
        info[3] = 1;
        for (int i = tId; i < unitNumber; i+=numberThread) {
            int xStart    = i * eP;
            auto aStart   = aHost + xStart * packUnit;
            core->MNNPackC4ForMatMul_A((float*)(tileHost), (const float**)(&aStart), info, stride);
            core->MNNPackedMatMul((float*)(cHost + xStart * packUnit), (float*)tileHost, (float*)bHost, parameters, postParametersPtr, (const float*)biasPtr);
        }
        if (tId != numberThread -1) {
            return;
        }
        if (xCount > 0) {
            stride[0] = xCount;
            stride[1] = parameters[1];
            info[2] = xCount;

            int xStart    = unitNumber * eP;
            auto aStart   = aHost + xStart * packUnit;
            // Copy
            core->MNNPackC4ForMatMul_A((float*)(tileHost), (const float**)(&aStart), info, stride);
            core->MNNPackedMatMulRemain((float*)(cHost + xStart * packUnit), (float*)tileHost, (float*)bHost, xCount, parameters, postParametersPtr, (const float*)biasPtr);
        }
    }, numberThread));

其中unitNumber为当前线程需要处理多少个unit，假设eP = 24，代表每个unit处理24个C4 Pack，假设numberThread=4，则unitNumber = (224 x 224) / 4 / eP = 522。即一个线程循环中对522个unit进行处理，不能整除的部分单独处理即可。

但是由于之前提到的mSupportMultiThread=false，numberThread实际上是恒为1。并不会在这一层级进行多线程划分。

对于单个unit的乘加操作，主要在于MNNPackC4ForMatMul_A和MNNPackedMatMul两个函数调用，如果看过这篇文章的话，其实这里跟Winograd的单个tile的乘加操作其实是复用相同的函数。可以跳转去看，这里不再贴上代码。

`MNNPackC4ForMatMul_A`函数重排 $A$ 矩阵

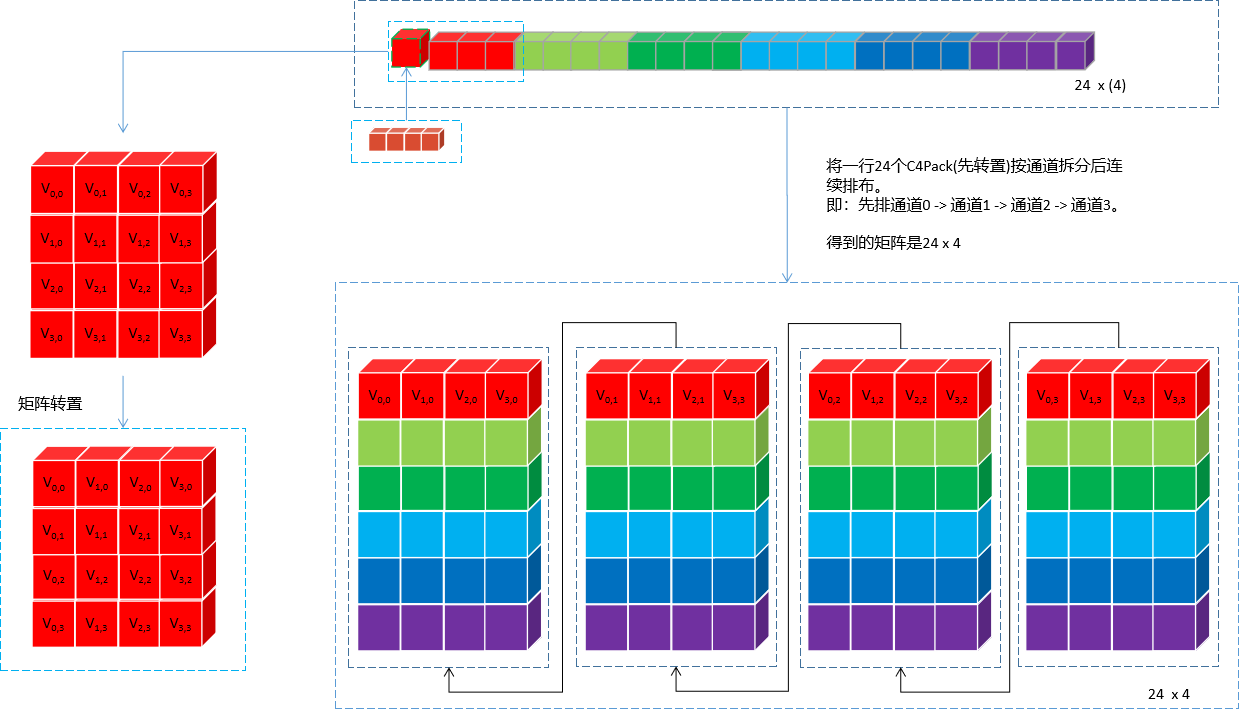
将单个C4通道的24个C4 Pack数据执行通道分离，属于同一个输入通道的24个值排在一起。两个C4通道（8个输入通道）处理完的示意图如下（24 x 8）：

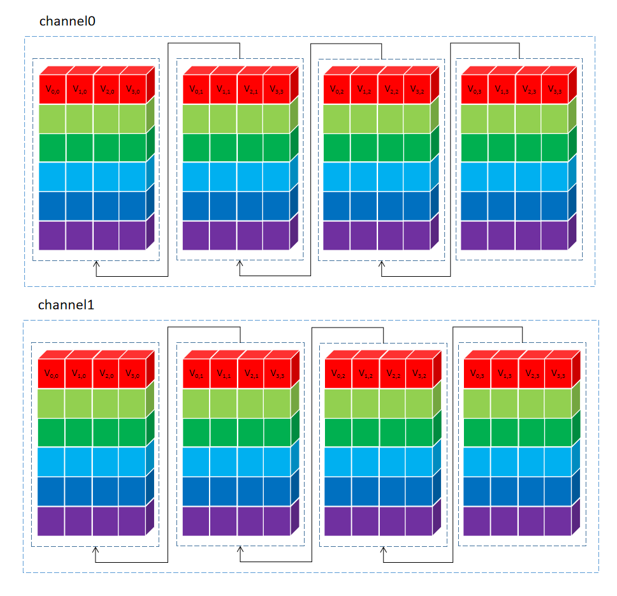
MNNPackedMatMul 矩阵乘加

为了解释起来更简单，从上面权重图中拿1个8 x C4 Pack（即：4个卷积核）来，至于所有的4个8 x C4 Pack（即：16个卷积核）卷积核循环4次处理即可。取出来的Mul+Add运算图如下：

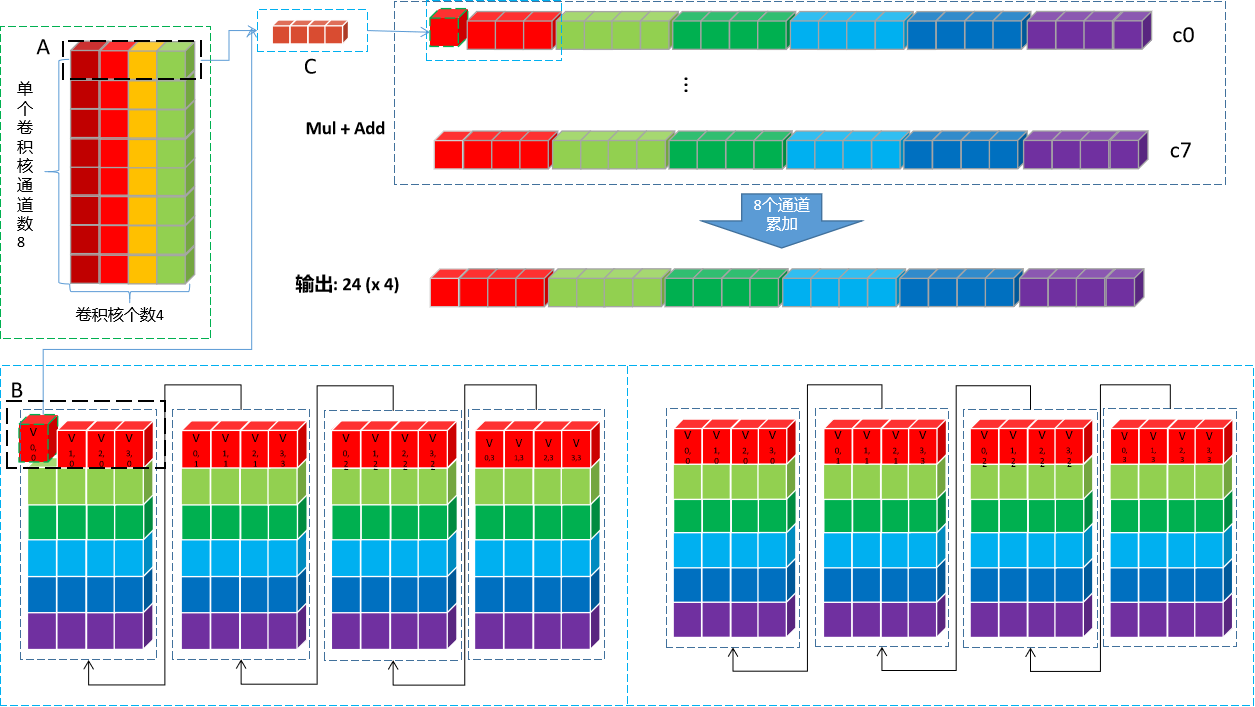
上图中的计算流程归纳一下：

1. MUL操作时，以上图中两个黑色框为计算单元。输入的黑色框中每次取一个值出来，与权重第一行黑色框中4个值依次相乘，并将结果pack到一起，直到24个值全部计算完成，输出一行24 (x 4)。
1. 输入更新到下一个通道24个值，权重也下移一行，重复8次上述运算。得到8 x 24 (x 4)。
1. 将8行数据对应位置累加(即：同一个卷积核的不同通道累加)，得到24个点一个C4 Pack的卷积结果：24 (x 4)。
1. 卷积核有16个，即：4个8 x C4 Pack，循环4次，将所有卷积核处理完，得到24个点所有卷积核的卷积结果：24 (x 4)

至此，就完成了一组unit的卷积操作，得到输出4 x 24 (x 4)。处理完所有的unit之后，就完成1 x 1的卷积操作。

post后处理

普通卷积的后处理

void _AVX_MNNPackedMatMulFMA(float* C, const float* A, const float* B, const size_t* parameter,
                             const float* postParameters, const float* bias) {
    auto h       = parameter[2];
    auto cStride = parameter[3] / sizeof(float);
#ifdef MNN_X86_USE_ASM
    if (postParameters == nullptr) {
        _AVX_MNNGemmFloatUnitMainFMA(C, A, B, parameter);
    } else {
        _AVX_MNNGemmFloatUnitMainFMA_Fused(C, A, B, parameter, postParameters, bias);
    }
    auto hC4          = UP_DIV(h, 4);
    auto hC8          = hC4 / 2;
    auto hR           = hC4 % 2;
    if (hR > 0) {
        auto zero = _mm_set1_ps(0.0f);
        // Set Last H4 = 0
        auto dst = C + hC8 * cStride;
        for (int x = 0; x < MNN_UNIT_E; ++x) {
            _mm_storeu_ps(dst + 8 * x + 4, zero);
        }
    }
#else
    _AVX_MNNPackedMatMul_Main(C, A, B, parameter);
    AVX2GemmPostTreat(C, MNN_UNIT_E, parameter, postParameters, bias);
#endif
}

在MNNPackedMatMul后，调用GemmPostTreat进行后处理。

递归过程中的后处理

if (!postParameters.empty() && COT.stackIndex >= 0) {
    if (1 == numberThread) {
        auto postFunction = [c11, COT, eSub, cHeight, numberThread, postParameters, core, this](int tId) {
            auto biasPtr = (const float*)(mStack[COT.stackIndex] + COT.offsetBytes);
            auto width = eSub * 2;
            auto height = cHeight * 2;
            auto c11Ptr = mStack[c11.stackIndex] + c11.offsetBytes;
            core->MNNAxByClampBroadcastUnit((float*)c11Ptr, (float*)c11Ptr, biasPtr, width, c11.lineStrideBytes / core->bytes, c11.lineStrideBytes / core->bytes, height, postParameters.data());
        };
        mFunctions.emplace_back(std::make_pair(postFunction, numberThread));
    } else {
        auto postFunction = [c11, COT, eSub, cHeight, numberThread, postParameters, core, this](int tId) {
            auto width = eSub * 2;
            auto height = cHeight * 2;
            auto c11Ptr = mStack[c11.stackIndex] + c11.offsetBytes;
            auto biasPtr = mStack[COT.stackIndex] + COT.offsetBytes;
            for (int y = tId; y < height; y+=numberThread) {
                core->MNNAxByClampBroadcastUnit((float*)(c11Ptr + y * c11.lineStrideBytes), (float*)(c11Ptr + y * c11.lineStrideBytes), (const float*)(biasPtr + y * core->bytes * core->pack), width, 0, 0, 1, postParameters.data());
            }
        };
        mFunctions.emplace_back(std::make_pair(postFunction, numberThread));
    }
}

由于递归过程构建中子矩阵的乘法调用_generateMatMul时传入的COT和postParameters均为空，如下：

auto code = _generateMatMul(eSub, lSub, hSub, X, Y, c21, Empty, currentDepth, {});

故实际上，除了递归顶层外，其他递归层次（包括普通卷积层）均不会执行后处理操作。当然，如果普通卷积就是顶层（即没有递归过程），那后处理由普通卷积负责完成。

onExecute

通过mFunctions队列依次执行onResize中构建的Strassen递归操作。

void StrassenMatrixComputor::onExecute(const uint8_t* AT, const uint8_t* BT, const uint8_t* COT, uint8_t* CT) {
    if (nullptr != AT) {
        mStack[0] = (uint8_t*)AT;
    }
    if (nullptr != BT) {
        mStack[1] = (uint8_t*)BT;
    }
    if (nullptr != CT) {
        mStack[2] = (uint8_t*)CT;
    }
    if (nullptr != COT) {
        mStack[3] = (uint8_t*)COT;
    }

    // All is done in onResize, just execute it
    for (auto& f : mFunctions) {
        MNN_CONCURRENCY_BEGIN(tId, f.second) {
            f.first(tId);
        }
        MNN_CONCURRENCY_END();
    }
}

困惑

实际上，在上述尺寸条件下，MNN并不会执行Strassen递归操作，而是直接执行普通卷积。因为Strassen虽然处理的数据规模越大，乘加计算上越有优势，但是在递归过程中访存操作比普通矩阵乘法要多的多，因此为了防止因为访存而引起可能的负优化，MNN每次递归都会对比两者的访存次数，选择访存次数更少的方法计算（即上面的终止条件2）。

MNN源码中cost之差是这样算的：

float AComputeCost = 4 * ((float)eSub * lSub);
float BComputeCost = 4 * (float)lSub * bHSub * hP;
float CComputeCost = 7 * (float)eSub * hSub;
float saveMatMulCost = (e / eP) * (aUnit * eP * hSub / core->pack + lSubUnit * eP * aUnit + lSub * bHSub * hP);

const float penalty = core->penalty;//FIXME: Find beter way to set it
float saveCost = saveMatMulCost - (AComputeCost + BComputeCost + CComputeCost) * penalty;
if (saveCost <= 0.0f) {
    return _generateBasicMatMul(e, l, h, AT, BT, CT, COT, postParameters);
}

化简一下其实为：

$\begin{align*} saveMatMulCost&=\frac{e}{ep}(\frac{ep}{2}*ic+\frac{ep}{2}*oc+\frac{ic*oc}{4}) \\ AComputeCost&=e*ic \\ BComputeCost&=ic*oc \\ CComputeCost&=\frac{7*e*oc}{4} \\ saveCost&=saveMatMulCost-\\&(AComputeCost+BComputeCost+CComputeCost)*penalty \\ \end{align*}$

但是不是对于其具体含义还是很困惑，已在github上提了issue，等大佬回复。

按照上述cost计算方法，在固定 $e=64×64, ep=24,penalty=1.5$ 的情况下，遍历 $ic\in[2,512],oc\in[2,512]$ ，实测下来会用到Strassen的都是ic和oc大于256的情况。

void TestStrassenCost() {
    int e = 64 * 64, ep = 24;
    float penalty = 1.5;
    std::ofstream fout("strassen_cost.txt");
    for (int ic = 2; ic <= 512; ic += 1) {
        for (int oc = 2; oc <= 512; oc += 1) {
            int origin_cost = e / ep * (ep / 2 * oc + ep / 2 * ic + ic * oc / 4);
            int strassen_cost = e * ic + ic * oc + (7 * e * oc) / 4;
            if (origin_cost - strassen_cost * penalty > 0) {
                fout << "use strassen, ic:" << ic << ", oc: " << oc << ", rate: " << origin_cost / (strassen_cost * penalty) << std::endl;
            }
        }
    }
    fout.close();
}