AI算法基础 [13]:初探Transformer
前言
Google论文:Attention Is All You Need
哈佛大神笔记:The Annotated Transformer
哈佛大神代码: annotated-transformer
本文主要参考了Alexander Rush大神这篇The Annotated Transformer,但并不是逐字翻译,而是加入了自己学习过程中的一些拙见和引申,如果不喜欢别人消化过的东西,可以直接阅读原文。Pytorch等框架其实已经实现了Transformer,至于为什么选择这篇文章进行学习而不是直接阅读Pytorch源码,是因为这篇不会包含出于框架本身考虑的过多的抽象和封装,且解读和代码兼而有之,作为Transformer学习的开篇,非常合适。
环境
代码所需的运行环境是python-3.6+pytorch-0.3.0(只有x86的linux版本),这里就用wsl的ubuntu环境做配置,刚好我的ubuntu是python3.6,否则可能就需要用conda配置虚拟环境+ipykernel生成jupyter notebook的kernel,大致如下(没有实操):
conda create -c conda-forge -n python3.6 python=3.6 |
由于我的wsl没有安装cuda,就不安装支持cuda的pytorch版本:
pip3 install https://download.pytorch.org/whl/cpu/torch-0.3.0.post4-cp36-cp36m-linux_x86_64.whl |
这里不太清楚为什么非要指定pytorch-0.3.0,可能文中使用的某些方法在后续版本更迭中被弃用了,为保证能完美复现,还是要严格按照上述要求配置环境。
背景
RNN模型的缺点是需要顺序计算,计算上很难实现并行。因而出现了Extended Neural GPU、ByteNet 和 ConvS2S等网络模型,这些都是以CNN作为构建基础,因此计算所有输入输出位置间的隐藏层表示可以做到并行。但这些模型也有缺点,就是随着距离的增长,将序列中两个位置(时刻)关联起来所需要的操作数也跟着增长。对于ConvS2S而言是线性增长,对ByteNet而言则是对数增长。这就导致很难学习到长距离之间的依赖关系。
Transformer引入了Self-Attention(Intra-Attention)机制,这是一种将序列的不同位置联系起来从而计算序列表示(representation)的注意机制。以机器翻译场景为例,它在编码每一个词的时候都能够注意(attend to)整个句子,从而可以解决长距离依赖的问题,同时计算Self-Attention可以用矩阵乘法一次计算所有的时刻,因此可以充分利用并行计算资源。
Transformer是第一个完全依靠Self-Attention机制,完全不使用序列对齐的RNN或卷积,来计算输入输出表示的转换模型。
模型结构
目前主流的神经序列转换(neural sequence transduction)模型要么是RNN一派,要么是带Encoder-Decoder的CNN一派。Transformer模型还通过Attention机制连接encoder和decoder。
所谓的序列转换模型就是把一个输入序列转换成另外一个输出序列,它们的长度很可能是不同的。比如基于神经网络的机器翻译,输入是法语句子,输出是英语句子,这就是一个序列转换模型。类似的包括文本摘要、对话等问题都可以看成序列转换问题。我们这里主要关注机器翻译,但是任何输入是一个序列,输出是另外一个序列的问题都可以考虑使用Encoder-Decoder模型。
Encoder将输入序列映射(编码)成一个连续的序列。而Decoder根据来解码得到输出序列,解码时一次生成一个元素,且每一步都是自回归(auto-regressive)的,即它会把前一个时刻的输出作为当前时刻的附加输入。
Encoder-Decoder基础架构
Encoder-Decoder结构模型的代码如下:
class EncoderDecoder(nn.Module): |
EncoderDecoder类定义了一种通用的Encoder-Decoder架构。具体的encoder,decoder,src_embed, tgt_embed,generator都是构造函数传入的参数,这样就方便我们对不同的实验更换不同的组件。
其中涉及了Embedding的概念,简单来讲就是用向量表示实体。例如RGB=(255, 255, 255)这一三维向量就是对白色这一颜色实体的Embedding。
Generator
Generator的代码如下:
class Generator(nn.Module): |
注意:Generator.forward返回的是softmax的log值。softmax函数定义如下:
其中:
- 为单个样本的全连接层输出分数logits,其尺寸应该与分类问题的类别数一致,对应第个类型的分数;
- 为分类问题的类别数;
softmax的作用简单来讲,就是将输出分数归一化到0-1,且所有类别分数之和为1。从概率论的角度可以将打分值解释为未归一化的对数概率,作为指数的幂就得了未归一化的概率,除法操作就是归一化的过程。
这里输出softmax的log值,可以配合nn.NLLLoss计算交叉熵损失(cross-entropy loss),也可以配合nn.KLDivLoss计算相对熵损失(Kullback-Leibler divergence loss)。交叉熵损失的定义如下:
其中:
- 为观测样本的数量;
- 为第个观测样本的交叉熵损失;
- 为符号函数,如果样本的真实类别为,则取1,否则取0;
- 为样本的输出分数中,对应到类别的分数;
NLLLoss(Negative Log Likelihood Loss)是计算负log似然损失(最大似然)。其配合F.log_softmax函数或nn.LogSoftmaxModule声明的callable对象可以等效为nn.CrossEntropyLoss。
KLDivLoss称为KL散度,又称相对熵,公式如下:
其中:
- 为第个样本的真值标签的概率分布(0-1,且和为1),对于分类问题而言,就是类别ID的one-hot编码,如总共5类,第个样本属于第4类,则为
[0,0,0,1,0]; - 为第个样本输出分数的概率分布(0-1,且和为1),与的shape相同;
若参照nn.KLDivLoss的定义,将当作输入,则上述公式可以简写为:
可以看出相对熵其实就是交叉熵减去信息熵。对于分类问题而言,真值标签的概率分布是确定的(非1即0),那么信息熵为0(即没有不确定性),这时相对熵其实就是交叉熵。
简单的验证代码如下:
x = torch.Tensor([4, 3, 2, 1, 0]).unsqueeze(0) |
这里需要注意的nn.KLDivLoss的reduction='mean'与其他模块不同,它表示在对batch(上例=1)和dimension(上例=5)尺度上做平均(即对每个输入元素平均),而reduction='batchmean'才是在batch维度上做平均。pyTorch会在下一个release版本中将其与其他模块进行统一。
Transformer
Transformer模型也是遵循上面的架构,如下图所示,只不过它的Encoder(左侧)是N个EncoderLayer组成,每个EncoderLayer包含一个Self-Attention SubLayer层和一个全连接SubLayer层。而它的Decoder(右侧)也是N个DecoderLayer组成,每个DecoderLayer包含一个Self-Attention SubLayer层、Attention SubLayer层和全连接SubLayer层。
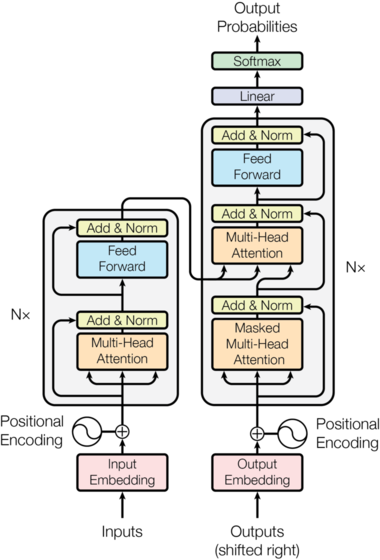
Encoder and Decoder Stacks
如前所述,Encoder和Decoder都是由N个相同结构的Layer堆积(stack)而成。因此我们首先定义clones函数,用于克隆相同的Layer。
def clones(module, N): |
这里使用了nn.ModuleList,ModuleList就像一个普通的Python的List,我们可以使用下标来访问它,它的好处是传入的ModuleList的所有Module都会注册到PyTorch里,这样Optimizer就能找到这里面的参数,从而能够用梯度下降更新这些参数。但是nn.ModuleList并不是nn.Module(的子类),因此它没有forward等方法,我们通常要把它放到某个Module里。
Encoder
Encoder就是N=6个EncoderLayer的stack,最后加上一个LayerNorm。
class Encoder(nn.Module): |
LayerNorm
LayerNorm不是BatchNorm,与BatchNorm区别在于归一化的维度不同,LayerNorm也存在可学习参数和,只是其为特征维度,而不是Batch维度。其实现代码如下(也可以用nn.LayerNorm):
class LayerNorm(nn.Module): |
EncoderLayer
按照原始论文的模型,EncoderLayer中每个残差连接后都接一个LayerNorm。单个EncoderLayer的构成为:
The Annotated Transformer稍微做了一些修改,将LayerNorm放到SubLayer之前,在SubLayer之后加了一个dropout层。构成如下:
由于这里把LayerNorm放到了SubLayer之前,所以上面在整个Encoder最后一层后面又再加了一个LayerNorm。总体来看,这里的实现与原论文中是基本一致的,只是对最开始的输入多做了一次LayerNorm。
SublayerConnection
有上面构成流程图可以看出,无论SubLayer是Self-Attention还是Dense,其前后相关的处理流程都是相同的。这里将SubLayer及其相关操作封装为SublayerConnection类:
class SublayerConnection(nn.Module): |
这个类会构造LayerNorm和Dropout,但是Self-Attention或者Dense并不在这里构造,还是放在了EncoderLayer类里,在forward的时候由EncoderLayer传入。这样的好处是更加通用,比如Decoder也是类似的需要在Self-Attention、Attention或者Dense前面后加上LayerNorm和Dropout以及残差连接,我们就可以复用SublayerConnection的代码。
EncoderLayer
class EncoderLayer(nn.Module): |
为了复用,这里的self_attn层和feed_forward层也是传入的参数,这里只构造两个SublayerConnection类对象。forward首先调用self.sublayer[0],这是SublayerConnection类的callable对象,最终会调用SublayerConnection类的forward方法。这个方法接受2个参数,一个是输入Tensor,一个是SubLayer的callable对象。在SublayerConnection.forward中,这个 callable对象仅接受一个参数,而self_attn需要4个参数(Query的输入,Key的输入,Value的输入和Mask),不过在Encoder中前3个参数都是输入Tensor,故这里通过lambda函数将self_attn再封装一层,就可以看成只有一个参数x的函数了(mask看成Constance)。
Decoder
class Decoder(nn.Module): |
Decoder也是N=6个DecoderLayer的stack,参数layer是DecoderLayer,它也是一个callable对象,最终__call__会调用DecoderLayer.forward方法,这个方法(后面会介绍)需要4个参数,输入Tensor(x),Encoder层的输出Tensor(memory),输入Encoder的Mask(src_mask)和输入Decoder的Mask(tgt_mask)。所以这里的Decoder.forward也需要这4个参数。
DecoderLayer
class DecoderLayer(nn.Module): |
DecoderLayer比EncoderLayer多了一个src-attn层,这是Decoder解码时注意(attend to)Encoder的输出(memory)。src-attn和self-attn的实现是一样的,只不过使用的Query,Key和Value输入不同。普通的Attention(src-attn)的Query是前面的SubLayer输入进来的(即来自self-attn的输出),Key和Value则是Encoder最后一层的输出memory;而Self-Attention的Query,Key和Value都是来自前一层的输出。
subsequent_mask
此外Decoder的self-Attention还有一点与Encoder的self-Attention不同:Decoder在解码t时刻的时候应当只能注意(attend to)1~t时刻的输入,而不能使用t+1时刻及其以后的输入。我们定义了subsequent_mask函数来生成Mask矩阵,代码如下:
def subsequent_mask(size): |
函数输出为一个下三角方阵,对角线及以下为1。每一行代表一个时刻的序列Mask。函数首先通过np.triu生成上三角阵,然后通过matrix==0把0变成1,把1变成0。
Multi-Head Attention
Attention
Attention(包括Self-Attention和普通的Attention)可以看成一个函数,它的输入是Query、Key、Value和Mask,输出是一个Tensor。其中输出是Value的加权平均,而权重通过Query和Key计算得到。具体的计算如下图所示,计算公式为:
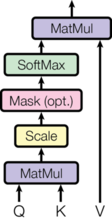
最常用的两种Attention分别是Additive Attention和Dot-Product(Multiplicative) Attention。这里使用的其实是带scaling factor()的dot-product attention,因此称为Scaled Dot-Product Attention。虽然两者在计算复杂度上是大致相当的,但是由于在实践中矩阵乘法有着高度优化的代码实现,所以后者在时间/空间性能上更具优势。
当的值较小时,Additive Attention和Dot-Product Attention的精度表现是相当的,但随着值增大,Additive Attention的表现会优于Dot-Product Attention。这可能是由于随着特征尺度的增大,矩阵乘法运算的内积值的数量级越来越大(为啥?假设参与点积的和中的元素符合均值为0,方差为1的随机分布,则它们的点积的均值为0,方差为),更容易落到softmax函数梯度较小的区域,造成梯度消失。因此加入了来调整内积大小。
代码如下:
def attention(query, key, value, mask=None, dropout=None): |
下面以一个实际的例子对上述代码进行理解。
假设Q的shape为
(30,8,33,64),其中30为batch,8为head个数(后面会讲何为head),33为序列长度,64为每个时刻的特征向量长度。K和Q的shape必须相同,而V可以不同,但这里的实现也是相同的。
d_k = query.size(-1) |
这两行代码实现了公式中的,不同的是,公式中的和指的是二维矩阵,而代码中query和key是4D-Tensor,包含了batch和head维度。torch.matmul只会对Tensor的最后两个维度执行矩阵乘法。则输出的scores的shape为(30,8,33,33),要怎么理解呢?抛开前两个维度不看,那么对于一个shape为(33,33)的attention矩阵而言,就表示时刻注意(attend to)时刻的得分(未经过softmax归一化)。
if mask is not None: |
这两行代码将scores矩阵中对应到mask为0的位置的值置为一个很小的负值,这样后面经过softmax函数后,该位置的概率就是一个无限接近0的值()。
对于不同的Attention,mask的shape是不同的:
- Encoder Self-Attention和Decoder的普通Attention:
mask的shape为(30,1,1,33),因为8个head的Mask都是一样的,所以第二维为1。第三维为1是因为每个时刻都可以注意(attend to)其他任意时刻(为1的维度在执行加减/逻辑运算时会自动broadcasting)。那有人就会问了,既然都可以attend to 所有时刻了,还要mask干嘛?首先是为了(函数设计)计算形式统一,还有就是因为30个batch的序列长度的最大值为33,不足33的样本会在序列后做padding,mask可以将padding的部分屏蔽掉。 - Decoder Self-Attention:
mask的shape为(30,1,33,33),每个时刻对应(33,33)矩阵的一行,对于序列长度不满33的样本,例如长度为30,则要对subsequent_mask(30)的输出矩阵做padding,右侧做3列zero-pad(假设pad值为0),下侧做最后一行外翻的padding(其实后面可以看到,下侧做什么padding都无所谓,在标签平滑时标签为pad值的整行概率分布都会被置0)。
p_attn = F.softmax(scores, dim = -1) |
对scores求softmax,将得分转化为归一化的概率分布p_attn。如果有dropput,还要对p_attn进行dropout(这也是原论文中没有的)。
return torch.matmul(p_attn, value), p_attn |
最后对p_attn和value(的最后两维)做矩阵乘法,p_attn的shape为(30,8,33,33),value的shape为(30,8,33,64),返回Tensor的shape为(30,8,33,64)。
Muilt-head
所谓Multi-head,就只是多做几次同样的事情(参数不共享),然后把结果拼接。对于每一个Head,都使用三个权重矩阵,和把输入转换成,和。然后对每一个Head进行Attention的计算,然后把N个Head的Attention输出拼接起来,最后用一个权重矩阵把输出压缩一下。用公式表示如下:
其中,,,,为head个数,为key的特征向量长度,为value的特征向量长度,为输入特征向量长度。具体到我们的例子中,,。具体的结构如下图:
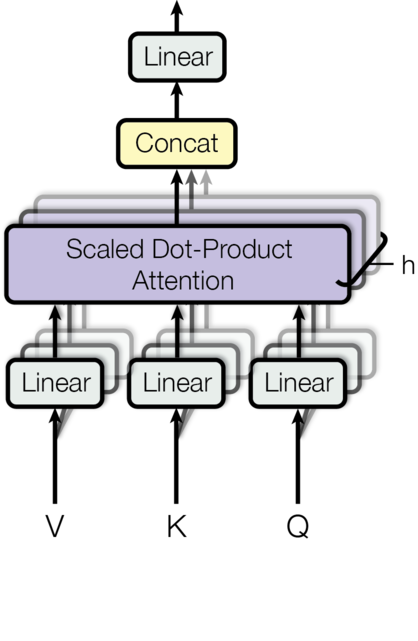
输入,和经过多个并行的线性变换后得到h(8)组Query,Key和Value,然后使用Self-Attention计算得到个向量,然后(在特征向量维度,即-1维)拼接起来,最后使用一个线性变换进行降维(这里,其实只是将特征向量维度恢复到与原始输入相同)。
代码如下:
class MultiHeadedAttention(nn.Module): |
首先看__init__构造函数,这里d_model为512,是输入Tensor特征向量维度的大小,也是输出Tensor特征向量维度的大小。因为有h(8)个head,所以每个head的d_k和d_v为512/8=64。接着我们构造了4(3个用于,和线性转换,1个用于输出的线性转换)个输入特征长度为d_model,输出特征长度也为d_model的全连接层列表self.linears,最后构造了一个dropout层。
然后来看forward方法,拆解如下:
if mask is not None: |
输入的mask的shape为(batch,1,seqlen)(Self-Attention)或者(batch,seqlen,seqlen)(Attention),通过unsqueeze(1)将其变为(batch,1,1,seqlen)(Self-Attention)或者(batch,1,seqlen,seqlen)(Attention),如前所述。
query, key, value = \ |
这一步完成输入,和的线性转换。zip将self.linears和(query, key, value)打包成元组列表,元素个数与最短列表一致,即返回[(self.linears[0],query),(self.linears[1],key),(self.linears[2],value)]。以第一组为例,l(x)相当于self.linears[0](query),即对query执行线性变换,输入query的shape为(batch,seqlen,512),线性变换后其实还是(batch,seqlen,512),然后通过view将其变成(batch,seqlen,8,64),然后通过transpose转换成(batch,8,seqlen,64)。这就是attention所要求的输入shape。同理可以完成对key和value的线性变换。
x, self.attn = attention(query, key, value, mask=mask, |
调用attention函数,计算得到x和self.attn。x的shape为(batch,8,seqlen,64),而self.attn的shape为(batch,8,seqlen,seqlen)。
x = x.transpose(1, 2).contiguous().view(nbatches, -1, self.h * self.d_k) |
transpose将x的shape转换为(batch,seqlen,8,64),contiguous为了解决transpose后Tensor不连续的问题,然后通过view转换成(batch,seqlen,512)。最后通过self.linears[-1]对x进行线性变换,输出shape依然是(batch,seqlen,512)。
应用
在Transformer里,有3个地方用到了Multi-Head Attention:
- Encoder的Self-Attention层:
query,key和value都是相同的值,来自Encoder中上一层的输出。每个时刻都可以attend to所有时刻的信息,即mask全1(padding除外)。 - Decoder的Self-Attention层:
query,key和value都是相同的值,来自Decoder中上一层的输出。每个时刻仅可attend to当前时刻之前的信息,即mask为下三角阵。 - Encoder-Decoder的普通Attention层:
query来自Decoder中上一层的输出,而key和value相同,均来自Encoder最后一层的输出。每个时刻都可以attend to所有时刻的信息,即mask全1(padding除外)。
全联接子层(Position-wise Feed-Forward Networks)
全联接子层由2个线性变换及它们之间的Relu激活构成,公式如下:
代码如下:
class PositionwiseFeedForward(nn.Module): |
其中,FFN的输入输出的特征向量维度d_model为512,隐藏层的特征向量维度d_ff为2048,在两个线性变换之间除了Relu还用了一个dropout。
Embedding和Softmax
与其他序列转换模型一样,输入的词序列都是字典ID序列,因此需要通过Embedding转化成d_model维的特征向量,源语言和目标语言都需要Embedding。代码实现如下:
class Embeddings(nn.Module): |
这里forward方法中除了通过nn.Embedding对输入x进行Embedding外,还乘上了。
此外还需要将Decoder的输出Tensor转化成预测下一个词的概率分布,这就是通过前面提到的包含了softmax的Generator实现的。
位置编码(Positional Encoding)
由于我们的模型不包含任何RNN和CNN,也就没有任何提取序列位置信息的能力,所以需要要给序列注入一些关于相对位置或绝对位置的信息,因此引入了位置编码(Positional Encoding)。位置编码与embedding得到的特征向量有相同的维度d_model,因此两者可以通过相加的方式完成位置信息的注入。在这里,使用以下公式生产位置编码:
其中,代表序列位置序号,代表特征向量的偶数维,代表特征向量的奇数维。位置编码本身是表征绝对位置的信息,选择这种方式进行位置编码的好处就是:可以表示成的线性函数(),也就提供了表达相对位置信息的能力。
位置编码的代码如下:
class PositionalEncoding(nn.Module): |
计算过程与公式一一对应,不再赘述。这里是通过register_buffer函数将pe保存下来。register_buffer通常用来保存一些模型参数以外的值。比如在BatchNorm中,我们需要保存running_mean(Moving Average),它不是模型的参数(不用做梯度下降),但是模型会修改它,而且在推理的时候也要使用它。这里也是类似的,pe是一个提前计算好的常量,我们在forward要用到它。如果我们保存(序列化)模型到磁盘的话,PyTorch框架也会帮我们保存buffer里的数据到磁盘,这样反序列化的时候能恢复它们。
完整模型
构造完整模型的代码如下:
def make_model(src_vocab, tgt_vocab, N=6, |
其中,src_vocab是源语言字典词数,tgt_vocab是目标语言字典词数。
首先将copy.deepcopy重命名为c,使得后续代码能简介一点。
然后构造了MultiHeadedAttention、PositionwiseFeedForward和PositionalEncoding类的对象attn、ff和position。
最后构造EncoderDecoder类对象,需要encoder、decoder、src_embed、tgt_embed和generator5个参数:
encoder/decoder:由N个EncoderLayer/DecoderLayer组成,而EncoderLayer/DecoderLayer还需要传入attn(DecoderLayer的self-atten和src-atten结构相同,只是输入不同)和ff这些SubLayer,因为这些SubLayer的结构相同,只需要通过deepcopy拷贝一份,而不需要重新构造。src_embed/tgt_embed:由一个Embeddings层和位置编码层c(position)组成。generator:直接构造就行了。
训练
Batches and Masking
class Batch: |
Batch类构造函数的输入为src、trg和pad,src为源语言样本,trg为目标语言的样本,可以为None,因为推理阶段不需要。
举个例子,假设要构建一个训练阶段的Batch,src的shape为(48,20),48为batch大小,20为最长句子长度,长度不足的句子用pad填充成长度20。trg的shape为(48,25),表示翻译后最长句子为25个词,同样长度不足也会用pad做padding。
self.src是Encoder的输入。self.src_mask将src中所有不等于pad值的位置都置为1,表示可以attend to除pad值外所有时刻。unsqueeze(-2)将src_mask的shape转换为(48,1,20),这符合上面MultiHeadedAttention.forward输入mask的尺寸要求。
self.trg和self.trg_y分别为Decoder的输入和输出损失计算时的真值标签,两者的shape均为(48,24),一个去尾,一个掐头,这样Decoder的输出就为已知当前时刻词,预测下一时刻词在字典中的概率分布。举个实际的例子,假设trg为<sos> it is a good day <eos>,则self.trg为<sos> it is a good day,而self.trg_y为it is a good day <eos>。
self.trg_mask通过make_std_mask函数得到,其中会调用前面介绍的subsequent_mask生成下三角阵,注意这里在逻辑与运算前,tgt_mask的shape为(48,1,24),而下三角阵的shape为(1,24,24),这里的逻辑与运算同样是利用了pytorch的广播机制,输出的tgt_mask的shape为(48,24,24)。
训练循环
def run_epoch(data_iter, model, loss_compute): |
上面是训练一个epoch的代码。遍历一个epoch中所有的batch,调用model.forward方法做前向推理,其中输入参数model即为make_model函数构建的完整模型。然后通过loss_compute计算损失和反向传播,参数是模型的预测out,真值标签batch.trg_y和batch中所有有效词的个数batch.ntokens。loss_compute是后面两个例子中定义的SimpleLossCompute类或MultiGPULossCompute类的callable对象,MultiGPULossCompute类比较复杂,实现了多GPU的训练。
训练数据和分批
- WMT 2014 English-German dataset:450万组句子对,字典词数37000;
- WMT 2014 English-French dataset:3600万组句子对,字段词数32000;
句子对根据句子长度进行分批,每个batch大约分别包含25000个源语言词和目标语言词。
global max_src_in_batch, max_tgt_in_batch |
这里定义了一个batch_size_fn函数,是用来作为后面重载自torchtext.data.Iterator的MyIterator类的参数,该函数返回新样本添加到batch中后,新的有效的batch size。这对动态调整batch size非常有用。
优化器
这里使用的是Adam算法,其中,,。并且会在训练过程中改变学习率,遵循以下公式:
大概的意思是,在(这里取4000)期间,学习率随着线性上升;之后便逐渐下降。实现代码如下:
class NoamOpt: |
一个关于学习率变化的例子如下:
# Three settings of the lrate hyperparameters. |
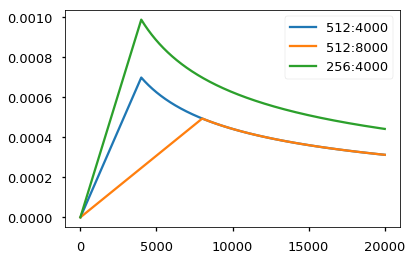
正则化
标签平滑(Label Smoothing)
这里使用了的标签平滑,会损害perplexty指标,但是可以提高精度和BLEU分数。
对于何为标签平滑,说人话就是将真值标签的概率分布从非0即1转变为真值的概率最大(),其他非真值(pad值除外)平均分享(县长来了,打土豪分田地啦)。这样做就是惩罚对某个结果非常确信的打分,避免过拟合。所以标签平滑也是一种正则化方法嘛。这里的代码实现如下:
class LabelSmoothing(nn.Module): |
首先看__init__构造函数,输入参数size指真值标签概率分布的长度,即词典大小;padding_idx指pad值在字典中的索引id;smoothing指要分出去的概率值。self.criterion选择了前面提到的相对熵损失,其他均为直接赋值,不再赘述。
再看forward方法,对输入x为Encoder-Decoder模型的输出(Generator输出的概率分布的log值)经过view转换的Tensor,shape为(batch_size*seq_len,vocab_size),target为真值标签(非one-hot形式),shape为(batch_size*seq_len)。具体操作拆解如下:
assert x.size(1) == self.size |
判断模型输出概率分布log值的长度是否等于词典大小;然后新建一个和模型输出shape相同的真值分布true_dist。
true_dist.fill_(self.smoothing / (self.size - 2)) |
将self.smoothing均分给self.size - 2个“农民”(-2是因为“土豪”占一个坑,“歪果仁”pad值占一个坑);将self.confidence分给由target认证的“土豪”;“歪果仁”毛都不给。
mask = torch.nonzero(target.data == self.padding_idx) |
序列长度较短的样本需要padding,其真值标签target的最后就会有pad值的ID,这时则需要将这一标签对应的整个概率分布全置为0,这很好理解,序列中padding位置本来就跟序列没关系,不需要参与损失计算。
self.true_dist = true_dist |
最后将模型输出的概率分布的log值x和标签平滑后的真值分布true_dist送给nn.KLDivLoss计算损失值。
可以结合下面这个例子来进一步加深理解:
# Example of label smoothing. |
crit.true_dist的值为:
[[0.0000, 0.1333, 0.6000, 0.1333, 0.1333],
[0.0000, 0.6000, 0.1333, 0.1333, 0.1333],
[0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]
画成heat-map则如下所示:

下面这个例子也进一步展示了标签平滑对过分相信某一选择的惩罚:
crit = LabelSmoothing(5, 0, 0.1) |
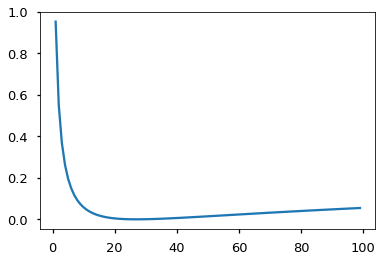
两个例子
原文作者还给了一简一繁两个训练的例子和一些其他的进阶玩法,这里暂时pass,有需要再看吧。
总结
这里只是对Transformer的基本理论和The Annotated Transformer中的代码实现做了一一对应的解读,只回答了是什么的问题,至于要回答为什么和怎么用的问题,道阻且跻。
参考
[2] Attention is All You Need 浅读(简介+代码)
[3] Transformer代码阅读
[4] Transformer详解








![现代硬件算法[8.8]: 时空局部性](/images/pd_09.webp)
![现代硬件算法[8.7]: 缓存遗忘算法](/images/pd_08.webp)
![现代硬件算法[8.6]: 淘汰策略](/images/pd_07.webp)
![现代硬件算法[8.5]: 列表排名](/images/pd_06.webp)
![现代硬件算法[8.4]: 外部排序](/images/pd_05.webp)