前言

可形变卷积网络（Deformable Convlution Networks, DCN）来自MSRA的研究团队提出的卷积结构。DCN的核心思想是将CNN中固定形状的卷积过程改变成了能适应物体形状的卷积过程，引入了学习空间几何形变的能力，来解决传统CNN对物体几何形变适应性差的问题。

基本思想

传统CNN在featureMap上做卷积操作时，它的感受野是固定的正方形形状。DCN的做法是对感受野上的每个点加一个偏移量，偏移的大小也通过学习获得，偏移后的感受野不再是固定矩形，而是与物体的实际形状相匹配。这样做的好处是无论物体形状怎么变，卷积的区域始终覆盖在物体形状的周围。如下图所示：

1

网络结构

DCN的网络结构如下图所示：

2

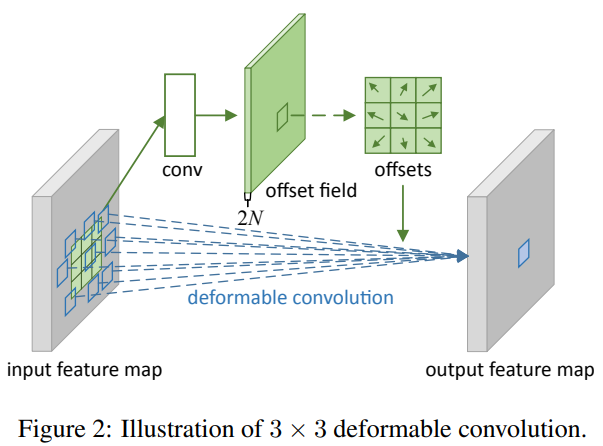
如上图所示，DCN的计算大致分两步：上方的conv层的输入为input feature map，用来学习offsets信息；下方的deformable conv层的输入为input feature map和offsets，先根据offsets插值出感受野的值，再进行卷积。

公式表示

普通卷积的公式表示如下：

y(p0)=∑pn∈ℜW(pn)⋅X(p0+pn)y(p_0) = \sum_{p_n \in \real}W(p_n)\cdot{X(p_0+p_n)}

其中，ℜ\real为卷积核的感受野，以dilation=1的3x3卷积核为例，则ℜ={(−1,−1),(−1,0),...,(0,1),(1,1)}\real = \{(-1,-1),(-1,0),...,(0,1),(1,1)\}；p0p_0为输出feature map上的位置，即卷积核的中心点；pnp_n为卷积核中每一点相对中心点的偏移量，是整数。

DeformConv的公式表示如下：

y(p0)=∑pn∈ℜW(pn)⋅X(p0+pn+Δpn)y(p_0) = \sum_{p_n \in \real}W(p_n)\cdot{X(p_0+p_n+\Delta p_n)}

在普通卷积公式基础上增加了一个偏移量Δpn\Delta p_n，即上面提到的通过Conv层学习到的offsets，一般为小数。故需要通过插值(一般为双线性插值)来获得感受野中X(p0+pn+Δpn)X(p_0+p_n+\Delta p_n)的值。

该研究团队后面又提出了DCN的改进版本Deformable ConvNets v2， V2认为感受野上的每个像素值对目标特征提取的贡献度是不一样的，因此引入了mask参数Δmk\Delta m_k来调节每个感受野值的权重。公式如下：

y(p)=∑k=1KWk⋅X(p+pk+Δpk)⋅Δmky(p)=\sum_{k=1}^K W_k \cdot {X(p+p_k+\Delta p_k)\cdot\Delta m_k }

推理框架支持情况

目前主流的开源推理框架对deformable conv算子的支持情况如下表：

推理框架 支持 实现方式
MNN × /
OpenPPL √ im2col+gemm
NCNN × /
TNN × /
OpenVINO √ im2col+gemm
Torchvision √ im2col+gemm

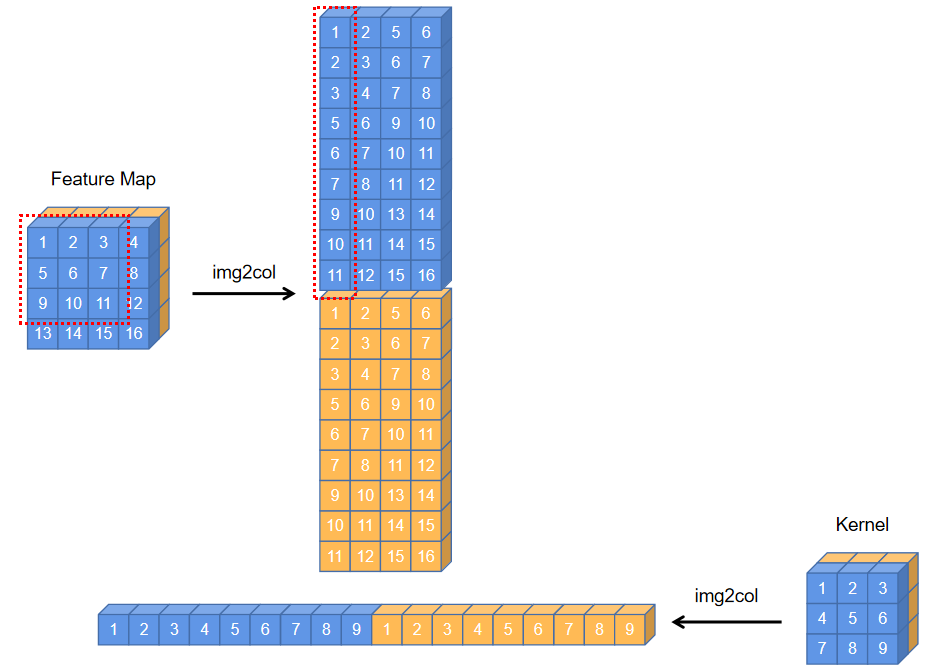
img2col

img2col的本质是用空间换时间，将原本不连续的内存转换成连续的，网上分析的有很多，这里不再赘述。放个简单的示意图方便自己对照：

3

GEMM

这个前面聊过很多了，可以翻看这里和这里。

参考

[1] Deformable Convolutional Networks

[2] Deformable ConvNets v2: More Deformable, Better Results