前言

Neon Intrinsics 是对ARM架构下的高级SIMD指令的拓展实现，本质是编译器知道其精确实现的函数。Neon Intrinsics是在arm_neon.h中定义的一组C/C++函数，由Arm编译器和GCC支持。这些函数让你不用直接编写汇编代码就可以使用Neon，因为这些函数本身包含内联到调用代码处的短汇编内核。此外，寄存器分配和流水线优化由编译器处理，从而避免了汇编程序员面临的许多困难。

Neon Intrinsics的优势：

  • 强大：内在函数使程序员无需手写汇编代码即可直接访问 Neon 指令集。
  • 移植性强：对于不同的目标处理器，手写的 Neon 汇编指令可能需要重写。但包含 Neon 内在函数的 C 和 C++ 代码 在新目标或新执行状态（例如，从 AArch32 迁移到 AArch64）下编译时，代码更改最少或无需更改。
  • 灵活：程序员可以按需切换使用 Neon 或者 C/C++，同时避免许多底层的工程问题。

Neon Intrinsics的劣势：

  • 跟直接使用库或通过编译器优化比，学习成本更高；
  • 跟手写汇编比，可能性能改善不能最大化；

函数检索

Neon Intrinsics 的使用可以通过官网检索，支持模糊搜索，支持通过汇编指令名搜索Intrinsics，以下图中加法指令为例，搜索结果依次包括操作描述，出参，对应汇编指令，入参，支持架构和伪代码。

1

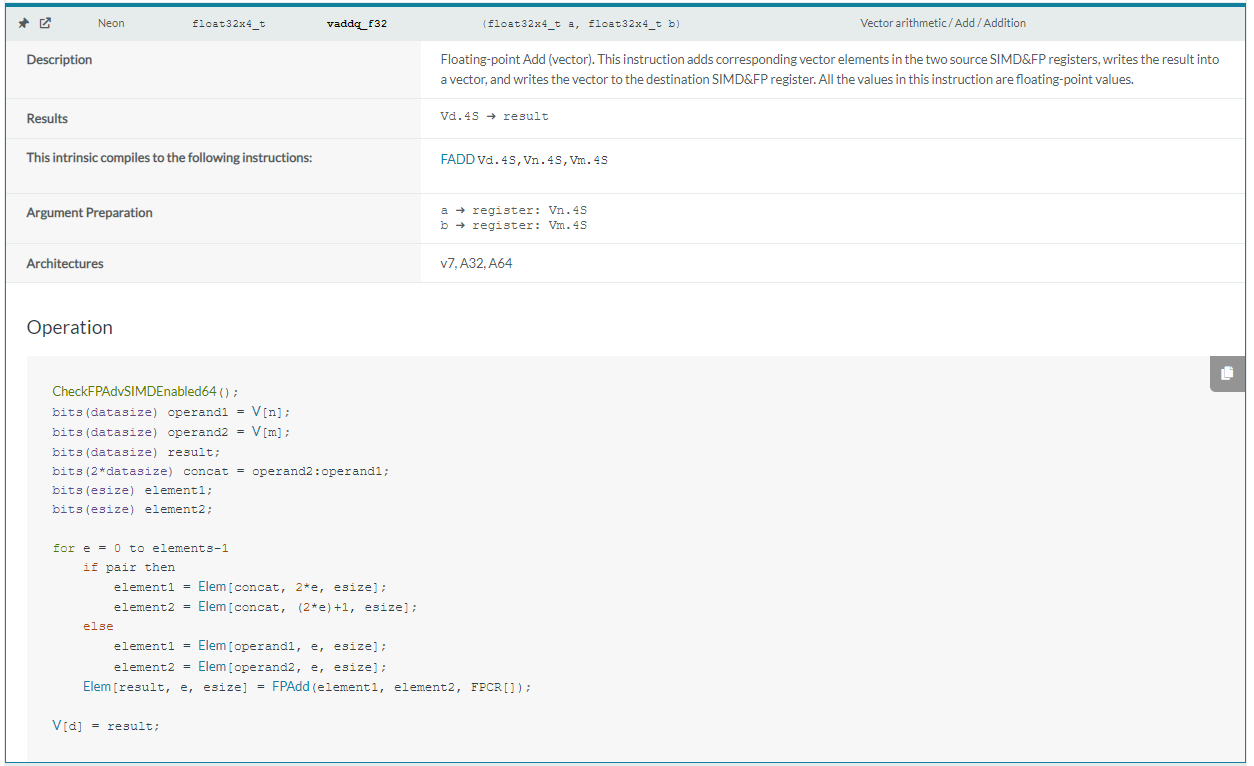
编程约定

宏（Macros）

当如下宏被定义并等于1时，代表对应的特性是可用的：

  • __ARM_NEON：编译器支持Advanced SIMD，对aarch64总为1；
  • __ARM_NEON_FP：支持 Neon 浮点操作，对aarch64总为1；
  • __ARM_FEATURE_CRYPTO：Crypto指令集可用，因此Cryptographic Neon intrinsics可用
  • __ARM_FEATURE_FMA：融合乘累加（Fused Multiply Accumulate）指令可用，因此使用了这些指令的Neon intrinsics可用。

类型（Types）

baseW_t： 标量数据类型

baseWxL_t：向量数据类型 对应64/128位寄存器

baseWxLxN_t：向量数组数据类型 对应那些在多个寄存器上操作的指令

其中：

  • base：数据的基础类型；
  • W：数据宽度（bits）；
  • L：向量数据类型中标量数据类型实例的数量；
  • N：向量数组类型中向量数据类型实例的数量；
  • 举例：float32x4x3_t

函数（Functions）

函数的一般表示如下：

ret v[p][q][r]name[u][n][q][x][_high][_lane | _laneq][_n][_result]_type(args)

其中：

  • ret：函数返回类型；
  • v：vector的缩写；
  • p: 表示成对操作（[value]可能会出现）；
  • q：表示饱和操作（除了AArch64操作中的vqtb[l][x]，其中q表示128位索引和结果操作数）（所谓饱和处理就是如果计算结果超出了要求的数据格式能存储的数据的最大值，那么就用最大值去表示这个数据，如果计算结果超出了要求的数据格式能存储的数据的最最小值，那么就用最小值去表示这个数据）；
  • r：表示舍入操作；
  • name：基本操作的描述性名称。这通常是一个高级SIMD指令，但也不总是；
  • u：表示有符号到无符号饱和；
  • n：表示收缩操作；
  • q：在name后表示对128位向量进行操作；
  • x：表示AArch64中的高级SIMD标量操作。它可以是b、h、s或d中的一个(即8、16、32或64位)；
  • _high：在AArch64中，用于涉及128位操作数的扩大和收缩操作。对于扩大128位操作数，high指源操作数的高64位；对于收缩，它指的是目标操作数的高64位；
  • _n：指示作为参数提供的标量操作数；
  • _lane：表示取自向量通道的标量操作数。 _laneq 表示从 128 位宽度的输入向量的通道中获取的标量操作数。 （ | 表示两者只会出现其中之一 ）；
  • type：主操作数类型的简写形式；
  • args：函数参数；

示例1：RGB通道分离

2

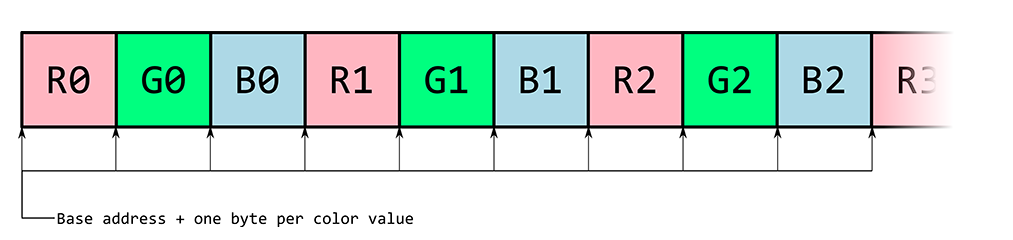
c代码实现：

void rgb_deinterleave_c(uint8_t *r, uint8_t *g, uint8_t *b, uint8_t *rgb, int len_color) {
    /*
     * Take the elements of "rgb" and store the individual colors "r", "g", and "b".
     */
    for (int i=0; i < len_color; i++) {
        r[i] = rgb[3*i];
        g[i] = rgb[3*i+1];
        b[i] = rgb[3*i+2];
    }
}

Neon Intrinsics 实现（未考虑corner case）：

void rgb_deinterleave_neon(uint8_t *r, uint8_t *g, uint8_t *b, uint8_t *rgb, int len_color) {
    /*
     * Take the elements of "rgb" and store the individual colors "r", "g", and "b"
     */
    int num8x16 = len_color / 16;
    uint8x16x3_t intlv_rgb;
    for (int i=0; i < num8x16; i++) {
        intlv_rgb = vld3q_u8(rgb+3*16*i);
        vst1q_u8(r+16*i, intlv_rgb.val[0]);
        vst1q_u8(g+16*i, intlv_rgb.val[1]);
        vst1q_u8(b+16*i, intlv_rgb.val[2]);
    }
}

示例2：矩阵乘法

3

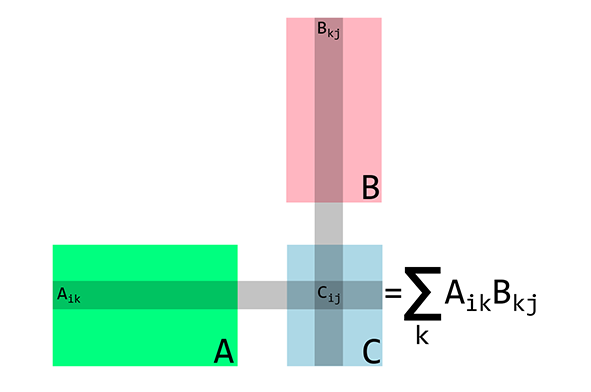
假设矩阵是按列存储的，nxm（n行m列）的矩阵M中元素索引方式为M_ij=M[n*j+i]

C实现（A矩阵nxk，B矩阵kxm，C矩阵nxm）：

void matrix_multiply_c(float32_t *A, float32_t *B, float32_t *C, uint32_t n, uint32_t m, uint32_t k) {
    for (int i_idx=0; i_idx < n; i_idx++) {
        for (int j_idx=0; j_idx < m; j_idx++) {
            C[n*j_idx + i_idx] = 0;
            for (int k_idx=0; k_idx < k; k_idx++) {
                C[n*j_idx + i_idx] += A[n*k_idx + i_idx]*B[k*j_idx + k_idx];
            }
        }
    }
}

Neon intrinsics实现（4x4矩阵）：

void matrix_multiply_4x4_neon(float32_t *A, float32_t *B, float32_t *C) {
        // these are the columns A
        float32x4_t A0;
        float32x4_t A1;
        float32x4_t A2;
        float32x4_t A3;
        
        // these are the columns B
        float32x4_t B0;
        float32x4_t B1;
        float32x4_t B2;
        float32x4_t B3;
        
        // these are the columns C
        float32x4_t C0;
        float32x4_t C1;
        float32x4_t C2;
        float32x4_t C3;
        
        A0 = vld1q_f32(A);
        A1 = vld1q_f32(A+4);
        A2 = vld1q_f32(A+8);
        A3 = vld1q_f32(A+12);
        
        // Zero accumulators for C values
        C0 = vmovq_n_f32(0);
        C1 = vmovq_n_f32(0);
        C2 = vmovq_n_f32(0);
        C3 = vmovq_n_f32(0);
        
        // Multiply accumulate in 4x1 blocks, i.e. each column in C
        B0 = vld1q_f32(B);
        C0 = vfmaq_laneq_f32(C0, A0, B0, 0);
        C0 = vfmaq_laneq_f32(C0, A1, B0, 1);
        C0 = vfmaq_laneq_f32(C0, A2, B0, 2);
        C0 = vfmaq_laneq_f32(C0, A3, B0, 3);
        vst1q_f32(C, C0);
        
        B1 = vld1q_f32(B+4);
        C1 = vfmaq_laneq_f32(C1, A0, B1, 0);
        C1 = vfmaq_laneq_f32(C1, A1, B1, 1);
        C1 = vfmaq_laneq_f32(C1, A2, B1, 2);
        C1 = vfmaq_laneq_f32(C1, A3, B1, 3);
        vst1q_f32(C+4, C1);
        
        B2 = vld1q_f32(B+8);
        C2 = vfmaq_laneq_f32(C2, A0, B2, 0);
        C2 = vfmaq_laneq_f32(C2, A1, B2, 1);
        C2 = vfmaq_laneq_f32(C2, A2, B2, 2);
        C2 = vfmaq_laneq_f32(C2, A3, B2, 3);
        vst1q_f32(C+8, C2);
        
        B3 = vld1q_f32(B+12);
        C3 = vfmaq_laneq_f32(C3, A0, B3, 0);
        C3 = vfmaq_laneq_f32(C3, A1, B3, 1);
        C3 = vfmaq_laneq_f32(C3, A2, B3, 2);
        C3 = vfmaq_laneq_f32(C3, A3, B3, 3);
        vst1q_f32(C+12, C3);
}

在上面的4x4矩阵相乘中，对于B的列，尽管我们可以使用同一个变量重新加载，但我们还是为B的列使用了唯一的变量名，这样做将提示编译器给这些变量分配不同的寄存器，使得处理器在等待另一列加载的同时完成当前列的算术指令。

Neon Intrinsics实现（一般矩阵）：

void matrix_multiply_neon(float32_t  *A, float32_t  *B, float32_t *C, uint32_t n, uint32_t m, uint32_t k) {
    /* 
     * Multiply matrices A and B, store the result in C. 
     * It is the user's responsibility to make sure the matrices are compatible.
     */     

    int A_idx;
    int B_idx;
    int C_idx;

    // these are the columns of a 4x4 sub matrix of A
    float32x4_t A0;
    float32x4_t A1;
    float32x4_t A2;
    float32x4_t A3;

    // these are the columns of a 4x4 sub matrix of B
    float32x4_t B0;
    float32x4_t B1;
    float32x4_t B2;
    float32x4_t B3;

    // these are the columns of a 4x4 sub matrix of C
    float32x4_t C0;
    float32x4_t C1;
    float32x4_t C2;
    float32x4_t C3;

    for (int i_idx=0; i_idx<n; i_idx+=4) {
        for (int j_idx=0; j_idx<m; j_idx+=4) {
            // Zero accumulators before matrix op
            C0 = vmovq_n_f32(0);
            C1 = vmovq_n_f32(0);
            C2 = vmovq_n_f32(0);
            C3 = vmovq_n_f32(0);
            for (int k_idx=0; k_idx<k; k_idx+=4) {
                // Compute base index to 4x4 block
                A_idx = i_idx + n*k_idx;
                B_idx = k*j_idx + k_idx;

                // Load most current A values in row 
                A0 = vld1q_f32(A+A_idx);
                A1 = vld1q_f32(A+A_idx+n);
                A2 = vld1q_f32(A+A_idx+2*n);
                A3 = vld1q_f32(A+A_idx+3*n);

                // Multiply accumulate in 4x1 blocks, i.e. each column in C
                B0 = vld1q_f32(B+B_idx);
                C0 = vfmaq_laneq_f32(C0, A0, B0, 0);
                C0 = vfmaq_laneq_f32(C0, A1, B0, 1);
                C0 = vfmaq_laneq_f32(C0, A2, B0, 2);
                C0 = vfmaq_laneq_f32(C0, A3, B0, 3);

                B1 = vld1q_f32(B+B_idx+k);
                C1 = vfmaq_laneq_f32(C1, A0, B1, 0);
                C1 = vfmaq_laneq_f32(C1, A1, B1, 1);
                C1 = vfmaq_laneq_f32(C1, A2, B1, 2);
                C1 = vfmaq_laneq_f32(C1, A3, B1, 3);

                B2 = vld1q_f32(B+B_idx+2*k);
                C2 = vfmaq_laneq_f32(C2, A0, B2, 0);
                C2 = vfmaq_laneq_f32(C2, A1, B2, 1);
                C2 = vfmaq_laneq_f32(C2, A2, B2, 2);
                C2 = vfmaq_laneq_f32(C2, A3, B2, 3);

                B3 = vld1q_f32(B+B_idx+3*k);
                C3 = vfmaq_laneq_f32(C3, A0, B3, 0);
                C3 = vfmaq_laneq_f32(C3, A1, B3, 1);
                C3 = vfmaq_laneq_f32(C3, A2, B3, 2);
                C3 = vfmaq_laneq_f32(C3, A3, B3, 3);
            }
            // Compute base index for stores
            C_idx = n*j_idx + i_idx;
            vst1q_f32(C+C_idx, C0);
            vst1q_f32(C+C_idx+n, C1);
            vst1q_f32(C+C_idx+2*n, C2);
            vst1q_f32(C+C_idx+3*n, C3);
        }
    }
}

参考

[1] Optimizing C Code with Neon Intrinsics