前言

非线性最小二乘法（NLS）是一种优化技术，可用于为包含非线性特征的数据集建立回归（回归即最佳拟合）模型。此类数据集的模型系数是非线性的。

NLS回归理论

在本文中将遵守如下的符号表示的惯例：

“帽子”符号用来表示在数据上拟合回归模型过程中生成的值，如 $\pmb{\hat{\beta}}$ 代表拟合系数的向量；

$\pmb{y_{obs}}$ 代表因变量y的观察值向量；

未加粗表示标量，加粗表示向量或矩阵。如 $y_{obs_i}$ 表示向量 $\pmb{y_{obs}}$ 中第 $i$ 个标量；

我们假设回归矩阵 $X$ 的尺寸为 $m \times n$ ，即它有 m 行 n 列回归变量。 $y$ 矩阵的尺寸为 $m \times 1$ ，系数矩阵的尺寸为 $n \times 1$ 或者 $1 \times n$ （转置形式）。

下面将看到3个可用MLS训练的非线性模型的例子：

例1

在下面这个模型中，回归系数 $\beta_1$ 和 $\beta_2$ 分别是2次幂和3次幂，所以模型的系数是非线性的：

$y_{obs} = \hat{\beta_0} + \hat{\beta_1^2} * x_1 + \hat{\beta_2^3} * x_2 + e$

其中， $e$ 表示模型残差，即观察值和预测值（ $\hat{\beta_0} + \hat{\beta_1^2} * x_1 + \hat{\beta_2^3} * x_2$ ）之间的差值。

例2

下面这个模型是一个自回归时间序列模型，其中 $\beta_0$ 和 $\beta_1$ 是相乘的关系，所以本质上也是非线性的：

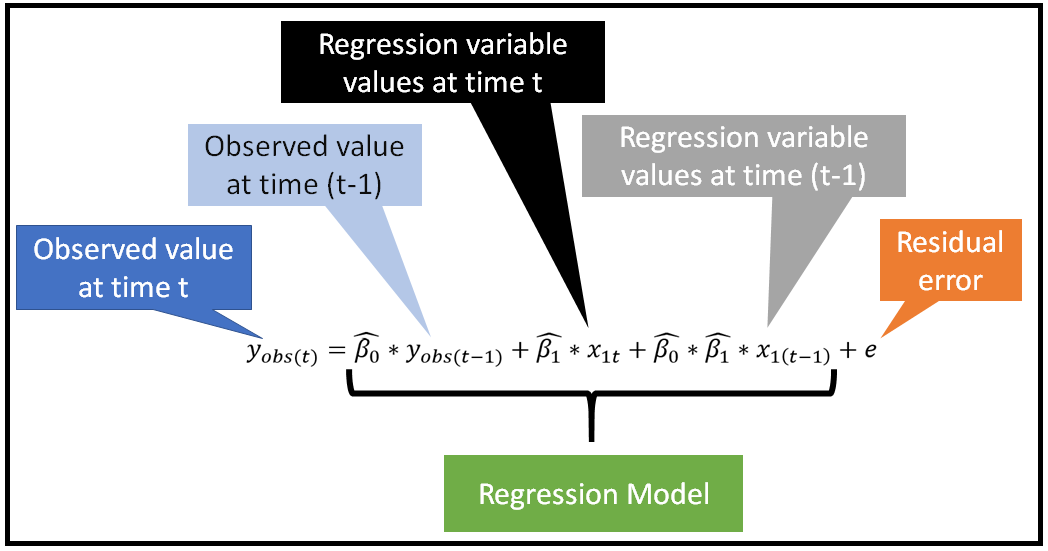
例3

在下面这个模型中，预测值是回归变量 $x$ 的线性组合的指数函数：

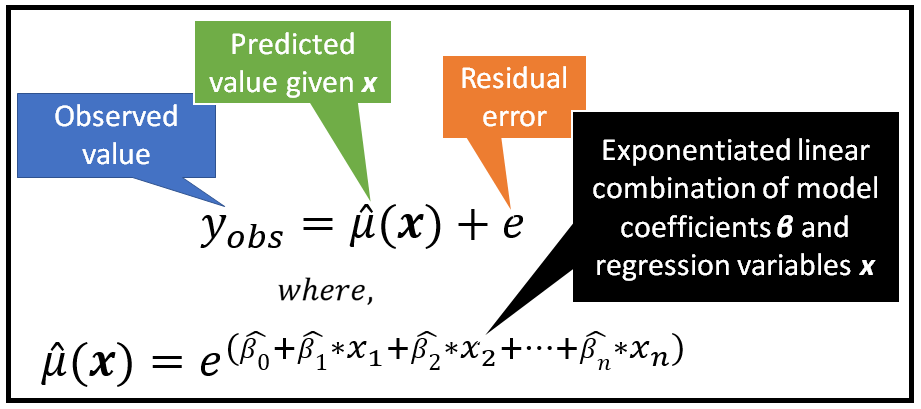
该公式常用于泊松回归模型或其衍化模型，如广义泊松模型或负二项式回归模型。具体来说，拟合均值 $\mu\_cap$ 表示为泊松概率分布的条件平均值，如下所示：

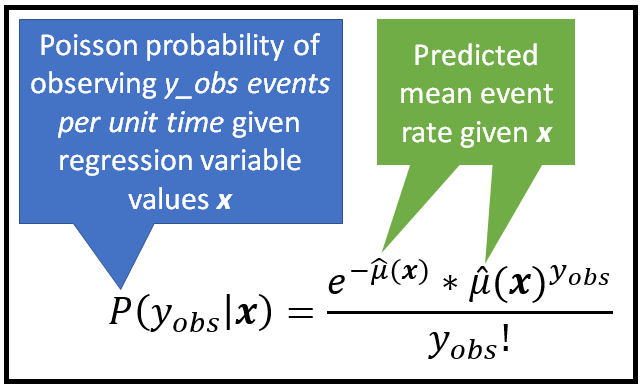
这种泊松回归模型用于拟合基于计数的数据集，如共享单车场景下，每天租用其中一辆自行车的人数。

NLS优化如何工作？

在NLS中，我的目标是寻找能最小化残差平方和（Residual Sum of Squares，RSS）的模型参数向量 $\pmb{\beta}$ ，换句话说，我们要减小：

$RSS = \sum_i^mr_i = \sum_i^m(y_{obs_i} - \hat{\mu_i})^2$

其中， $\hat{\mu_i}$ 是模型对数据集中第 $i$ 行的预测，是模型参数向量 $\pmb{\hat{\beta}}$ 和回归变量 $\pmb{x_i}$ 的函数，如下：

$\hat{\mu}(\pmb{x_i}) = f(\pmb{\hat{\beta}},\pmb{x_i})$

将其替换进上述RSS等式中：

$RSS = \sum_i^mr_i = \sum_i^m(y_{obs_i} - f(\pmb{\hat{\beta}},\pmb{x_i}))^2$

最小化RSS的一种方法就是对 $\pmb{\hat\beta}$ 求微分，对微分为0进行求解，即：

$\frac{\partial}{\partial\hat\beta_j}(RSS) = 0 \quad \forall j \in [1,n]$

由于 $\pmb{\hat\beta}$ 是一个长度为 n 的向量，对应于 n 个回归变量 $x_1$ ， $x_2$ ，… ， $x_n$ ，需要对每一个分量的偏微分为0进行求解，如下：

$\frac{\partial}{\partial\hat\beta_1}(RSS) = 0 \\ \implies \frac{\partial}{\partial\hat\beta_1}\sum_i^m(y_{obs_i} - f(\pmb{\hat{\beta}},\pmb{x_i}))^2 = 0 \\ \implies -2\sum_i^m(y_{obs_i} - f(\pmb{\hat{\beta}},\pmb{x_i})) * \frac{\partial f(\pmb{\hat\beta}, \pmb{x_i})}{\partial\hat\beta_1} = 0$

因为有 n 个参数从 $\hat\beta_1$ 到 $\hat\beta_n$ ，所以就得到了 n 个等式组成的方程组。但是，与普通最小二乘法（Ordinary Least Squares，OLS）估计不同，n 个方程组没有封闭形式的解。因此，需要使用迭代优化技术，在每次迭代中（迭代次数用 $k$ 表示），对参数 $\hat\beta_1$ 到 $\hat\beta_n$ 做一个微小的调整，如下所示，并重新评估RSS。

$\hat\beta_j^k = \hat\beta_j^{(k-1)} + \delta\hat\beta_j$

目前有几种算法可以用来有效地更新 $\pmb{\hat\beta}$ 向量，直到更新到一组最佳的值，以使得RSS最小化。其中主要是基于信赖域（Trust Region）的方法，如信赖域反射（Trust Region Reflective）算法、Levenberg-Marquardt 算法和Dogbox 算法。SciPy支持这三种算法。