现代硬件算法[1]: 渐进复杂度
复杂度模型(Complexity Models)
如果你打开了一本计算机科学的教科书,它可能在一开始就介绍了计算复杂度(computational complexity)。简单地说,计算复杂度是在计算过程中执行的所有基本操作(诸如加法、乘法、读取、写入等)的总和,可以根据不同操作的耗时进行加权。
复杂度是一个不算新的概念。20世纪60年代初它被系统地制定出来,此后被普遍用作估计算法成本的代价函数。这个模型之所以被如此迅速地采用,是因为它很好地近似了当时计算机的工作方式。
经典复杂度理论
CPU的“基本操作”称为指令(instructions),其“成本”称为延迟(latencies)。指令存储在内存(memory)中,并由处理器逐一执行,处理器的一些内部状态(state)存储在一组寄存器(registers)中。其中一个寄存器是指令指针(instruction pointer),它指示要读取和执行的下一条指令的地址。每一条指令都会以某种方式改变处理器的状态(包括指令指针的移动),可能会修改主内存,并需要占用若干CPU周期(CPU cycles)执行完成,之后才能启动下一条指令。
要估计程序的实际运行时间,我们就需要对其执行的所有指令的延迟进行求和,然后除以时钟频率(clock frequency),即特定CPU每秒执行的周期数。
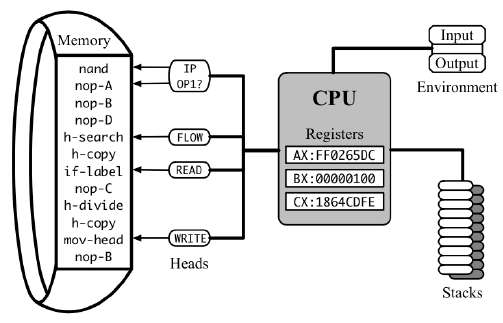
时钟频率是一个不稳定且通常未知的变量,它取决于CPU型号、操作系统设置、当前微芯片温度、其他组件的耗电情况以及许多其他因素。相比之下,当用时钟周期表示时,指令延迟是静态的,甚至有时在不同CPU之间也能保持一致。因此对它们进行计数对于分析更有用。
举个例子,标准定义下的矩阵乘法算法需要总共次算术运算,其中包括次乘法和次加法。如果我们查找这些指令的延迟(在被称为指令表(instruction tables)的特殊文档中,例如这个),我们可以发现,乘法需要3个周期,而加法需要1个周期,所以整个计算我们需要总共个时钟周期(这里我们暂且忽略了为给这些计算指令“提供”正确数据所需做的其他工作(即访存操作)的消耗)。
类似于指令延迟的总和可以作为与时钟频率无关的总执行时间的近似表示,计算复杂度可以用于量化抽象算法的内在时间要求,而不依赖于特定计算机的选择。
渐进复杂度(Asymptotic Complexity)
将执行时间表示为输入数据尺寸的函数,在现在看来习以为常,但在20世纪60年代并非如此。当时,典型的计算机耗资数百万美元,体积巨大以至于需要单独的房间,时钟频率以千赫兹为单位。它们被用于手头上的实际任务,比如预测天气、向太空发射火箭,或者计算苏联核导弹能从古巴海岸飞多远,所有这些都是有限长度的问题。那个时代的工程师主要关心如何计算3×3矩阵乘法而不是n×n矩阵乘法。
导致这一转变的原因是计算机科学家对计算机会一直更快抱有信心——事实上,情况确实如此。随着时间的推移,人们一开始不再对执行时间的计数,之后停止了对周期的计数,甚至停止了对计算操作的精确计数,取而代之的是一个估计值,它在足够大的输入上,只有不超过一个常数因子的偏差。通过渐进复杂度(Asymptotic Complexity),可以把冗长的个时钟周期转换为简单的,在“大O”中隐藏单个操作的初始成本,以及所有其他复杂的硬件参数。
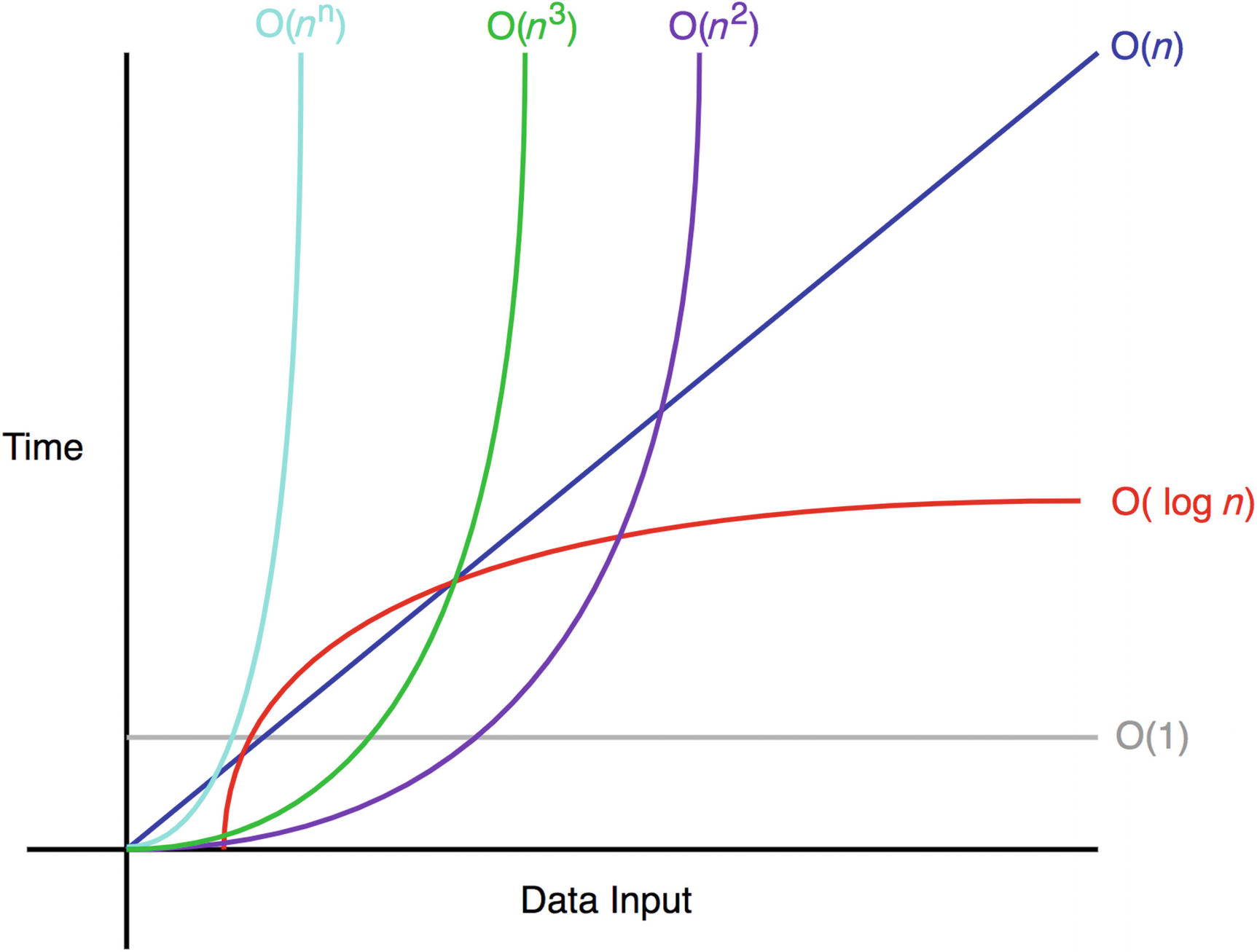
我们使用渐近复杂度的原因是,它在保持足够精确性的同时,提供了简单性,以在大型数据集上产生关于算法相对性能的有用结果。在计算机最终将变得足够快,以在合理的时间内处理任何足够大的输入的承诺下,无论隐藏常数是多少,渐近更快的算法在实时性上也总是更快。
但事实证明,这一承诺是不真实的——至少在时钟速度和指令延迟方面是不正确的——在本章中,我们将尝试解释为什么以及如何处理它。







