简介

Winograd算法起源于1980年，作者Shmuel Winograd 在文章《On multiplication of polynomials modulo a polynomial》中提出的减少FIR滤波器计算量的一个算法。他指出，对于输出个数为 $m$ ，参数个数为 $r$ 的FIR滤波器，不需要 $m×r$ 次乘法计算，而只需要 $u(F(m,r))=m+r-1$ 次乘法计算即可。

后来，有人发现此算法可以用来优化加速CNN网络的卷积计算《Fast Algorithms for Convolutional Neural Networks》，从此Winograd算法被广泛应用于各推理框架中。

原理

1D Winograd算法

1维卷积 $F(2,3)$ 为例，输入信号 $d=[d_0,d_1,d_2,d_3]^T$ ，卷积核 $g=[g_0,g_1,g_2]^T$ ，则卷积可以写成如下矩阵乘法形式：

$F(2,3)=\begin{bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \end{bmatrix} \begin{bmatrix} g_0 \\ g_1 \\ g_2 \\ \end{bmatrix} = \begin{bmatrix} r_0 \\ r_1 \end{bmatrix}$

如果这个计算过程使用普通的矩阵乘法，一共需要 6 次乘法和 4次加法。

但是，我们仔细观察一下，卷积运算中输入信号转换得到的矩阵不是任意矩阵，其有规律的分布着大量的重复元素，例如 $d_1$ 和 $d_2$ 。Winograd做了如下变换：

$F(2,3)=\begin{bmatrix} d_0 & d_1 & d_2 \\ d_1 & d_2 & d_3 \end{bmatrix} \begin{bmatrix} g_0 \\ g_1 \\ g_2 \\ \end{bmatrix} = \begin{bmatrix} m_1+m_2+m3 \\ m_2-m_3-m_4 \end{bmatrix}$

其中，

$m_1=(d_0-d_2)g_0 \quad m_2=(d_1+d_2)\frac{g_0+g_1+g_2}{2} \\ m_4=(d_1-d_3)g_2 \quad m_3=(d_2-d_1)\frac{g_0-g_1+g_2}{2}$

在CNN的推理阶段，卷积核上的元素是固定的，所以上式中和 $g$ 相关的式子可以提前在模型初始化阶段算好，整个推理阶段只用计算一次，因此可以忽略。所以这里一共需要 4次乘法和 8次加法。

上面其实就是1D的Winograd算法，我们将上面的计算过程写成矩阵的形式如下：

$Y=A^T[(Gg)\odot(B^Td)]$

其中，

$\odot$ 表示element-wise multiplication（Hadamard product），即对应位置相乘操作；
$g$ 表示卷积核；
$d$ 表示输入特征图；
$G$ 表示卷积核变换矩阵，尺寸为 $(u+k-1)×k$ ；
$B^T$ 表示输入变换矩阵，尺寸为 $(u+k-1)×(u+k-1)$ ；
$A^T$ 表示输出变换矩阵，尺寸为 $(u+k-1)×u$ ；
$u$ 表示输出尺寸， $k$ 表示卷积核尺寸， $su=(u+k-1)$ 表示输入尺寸。
各矩阵具体值如下：

$\begin{align*} & B^T=\begin{bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & -1 & 1 & 0 \\ 0 & 1 & 0 & -1 \end{bmatrix} \\ & G=\begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 1 \\ \end{bmatrix} \\ & A^T = \begin{bmatrix} 1 & 1 & 1 & 0 \\ 0 & 1 & -1 & -1 \\ \end{bmatrix} \\ & g = \begin{bmatrix} & g_0 & g_1 & g_2 \end{bmatrix}^T \\ & d = \begin{bmatrix} d_0 & d_1 & d_2 & d_3 \end{bmatrix}^T \end{align*}$

$G$ , $B^T$ , $A^T$ 三个变换矩阵的推导原理及过程可以参考：详解Winograd变换矩阵生成原理。当然，github有个工具wincnn可以直接帮我们计算。

2D Winograd算法

将 $F(2,3)$ 扩展到 $F(2×2, 3×3)$ ，形象的展示如下图：

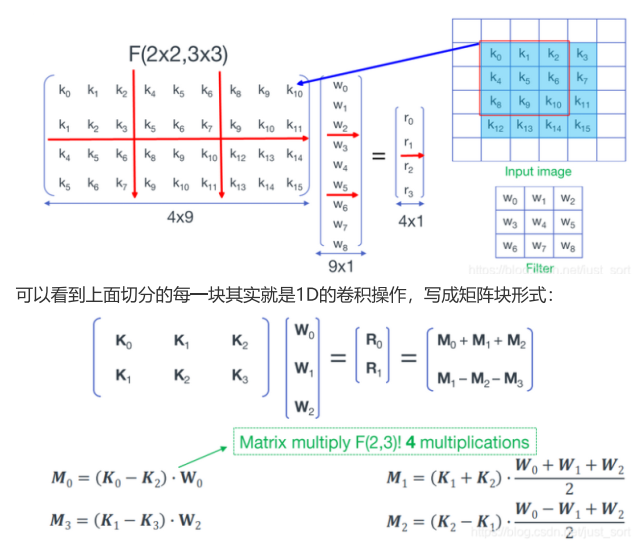
上图中最后得到 $M_0...M_3$ 的操作为4次矩阵加法和4次矩阵乘法，由 $M_0...M_3$ 得到 $[R_0, R_1]^T$ 为4次矩阵加法，同样 $W$ 矩阵的转换的计算量忽略不计。

$K_{0...3}$ 之间的4次矩阵加法，每次实际为4次加法（注意不要被上面扩展后的 $K$ 矩阵划分的小方块中6个元素所迷惑，其中有重复的元素），共 $4×4=16$ 次加法；
4次矩阵乘法可以转换为4次 1D Winograd 来计算，每次 1D Winograd 计算中有4次乘法，8次加法，共 $4×4=16$ 次乘法， $4×8=32$ 次加法；
最后 $M_0...M_3$ 之间的4次矩阵加法，由于 $M$ 矩阵的尺寸为 $2×1$ ，所以共 $4×2=8$ 次加法；
综上， $F(2×2, 3×3)$ 的Winograd算法共 $\color{OrangeRed}16 次乘法和 56次加法$ ，如果使用常规卷积运算，则需要 $\color{OrangeRed}36 次乘法和 32次加法$

上面的计算过程写成矩阵的形式如下

$Y = A^T[[GgG^T]\odot[B^TdB]]A$

1D 到 2D的公式推导

约定：大写字母或小写字母加上箭头均代表矩阵或向量， $K_0$ 与 $\overrightarrow{d_0}$ 均表示输入矩阵的第一行， $W_0$ 与 $\overrightarrow{k_0}$ 均表示卷积核的第一行

这里沿用2D Winograd推导中的字母表示，最后会转为1D Winograd推导中的字母表示

首先对上述公式进行重排，输出为 $2×2$ 矩阵：

$[R_0,R_1] = [M_0+M_1+M2, M_1-M_2-M3] \\ = [M_0,M_1,M_2,M_3]\begin{bmatrix} 1 & 0 \\ 1 & 1 \\ 1 & -1 \\ 0 & -1 \end{bmatrix} = [M_0,M_1,M_2,M_3]A$

结合上面计算代入 $M_n$ 得下式：

$\begin{align*} & [R_0,R_1] = \\ & \bigg[A^T[(GW_0)\odot(B^T(K_0-K_2))],A^T[(G\frac{W_0+W_1+W_2}{2})\odot(B^T(K_1+K_2))],\\ & A^T[(G\frac{W_0-W_1+W_2}{2})\odot(B^T(K_2-K_1))],A^T[(GW_2)\odot(B^T(K_1-K_3))]\bigg]A \\ & = A^T\bigg[[(GW_0)\odot(B^T(K_0-K_2))],[(G\frac{W_0+W_1+W_2}{2})\odot(B^T(K_1+K_2))],\\ & [(G\frac{W_0-W_1+W_2}{2})\odot(B^T(K_2-K_1))],[(GW_2)\odot(B^T(K_1-K_3))]\bigg]A \\ \end{align*}$

由于hadamard product（ $\odot$ ）和concat（ $,$ ）操作可以交换而不影响结果，因此：

$\begin{align*} & [R_0,R_1] = \\ & A^T\bigg[(G[W_0, \frac{W_0+W_1+W_2}{2}, \frac{W_0-W_1+W_2}{2}, W_2])\odot(B^T[K_0-K_2, K_1+K_2, K_2-K_1, K_1-K_3])\bigg]A \\ & =A^T\bigg[(G[W_0,W_1,W_2]\begin{bmatrix} 1 & \frac{1}{2} & \frac{1}{2} & 0 \\ 0 & \frac{1}{2} & -\frac{1}{2} & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} & 1 \end{bmatrix}) \odot(B^T[K_0,K_1,K_2,K_3]\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 1 \\ -1 & 1 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}) \bigg]A \\ & = A^T\bigg[(G[\overrightarrow{k_0},\overrightarrow{k_1},\overrightarrow{k_2}]G^T)\odot(B^T[\overrightarrow{d_0},\overrightarrow{d_1},\overrightarrow{d_2},\overrightarrow{d_3}]B) \bigg]A \\ & = A^T[(GKG^T)\odot(B^TDB)]A \end{align*}$

工程应用角度看

Winograd算法可以分为4个步骤：

1. 初始化期间完成卷积核的变换weightTransform，即： $GKG^T$
1. 运行期间完成输入数据的变换sourceTransform，即： $B^TDB$
1. 运行期间完成输入数据与权重的MatMul，即： $(GKG^T)\odot(B^TDB)$
1. 运行期间完成输出数据的变换dstTransform，即： $A^T[(GKG^T)\odot(B^TDB)]A$

关于计算量的讨论

关于1D Winograd，网上最常见的解释是：相比于普通的矩阵乘法，使用Winograd算法之后乘法次数减少2次，加法次数增多4次，实际使用中，乘法指令周期比加法要长，通俗来讲Winograd就是减少乘法操作，用更快的加法操作来达到加速目的。

但是这样的解释是有 $\color{OrangeRed}局限性$ 的：

其他分块情况

首先，上文中列举的是 $F(2,3)$ 的情况，查看变换矩阵得到，该情况下的输入、输出变换矩阵（ $A$ 和 $B$ ）系数非0即1（-1），此种情况下确实不需要乘法。
但对于 $F(4,3)$ ，或者 $F(6,3)$ 等block更大情况，变换矩阵中存在很多非0和1的系数，单独的MatMul乘法计算是减少了，但是引入了额外的输入、输出变换中需要的乘法，会存在乘法次数变多的情况，这个在原始论文中也有提及。

CPU架构

其次，关于浮点乘法比浮点加法指令周期长的问题，这个在旧的CPU架构下会存在，但是目前使用的CPU架构下，浮点的乘法和加法指令周期是一样的。
比如X86端 Intel CPU，从第5代Broadwell架构开始，两者的延迟就没有差别了，在intel core i7 9700 CPU（Coffee lake 第9代）上测试SSE指令集的浮点乘法和加法，经过实测，两者性能确实没有差异。
SSE指令集SIMD加法和SIMD乘法的对比可以点击跳转手册查看；
关于SSE指令集中所列出的两个属性latency（延迟）和throughput（CPI）吞吐量的具体含义可以看这里，我的理解就是：
- latency就是完成一条指令所需要的时间，即生成结果的指令与使用该结果的指令之间的周期数，比如Broadwell架构下_mm_add_ps浮点加法的latency为3，则表示（在不发生RAW冒险（数据冒险的一种，写后读冒险）的情况下）最快也要3个周期，其他指令才能获得浮点加法的运算结果。
- throughput吞吐量，又称CPI（cycle per instruction，每指令周期数），是发射一条指令所需要的时钟周期数，比如Broadwell架构下_mm_mul_ps浮点乘法的throughput为0.5，则表示一个时钟周期内可以发射2条浮点乘法指令。
- 比喻一下：延迟=水管中水的流速，吞吐量=水管的粗细

考虑多通道输入输出

实际要考虑卷积中的输入通道数 $IC$ ，输出通道数 $OC$ 。因为输入变换只与 $IC$ 有关，输出变换只与 $OC$ 有关。而普通滑窗卷积计算与 $IC$ ， $OC$ 均相关。

完整的计算量对比：

普通卷积：

$OriginalCost = OW*OH*OC(2*IC*kernelX*kernelY-1)$
Winograd卷积：

$\begin{align*} & SrcTransformCost = 2*su*M*IC \\ & MatMulCost = su*su*IC*OC \\ & DstTransformCost = (su+u)*N*OC \\ & WinogradCost = (SrcTransformCost+MatMulCost+DstTransformCost)*(OW/u)*(OH/u) \end{align*}$

其中：
- $u\in[2,8]$ 表示单个块的输出尺寸Unit；
- $su=u+kernel-1$ 表示单个块的输入尺寸Source Unit；
- $M\in(0,su*su)$ 表示输入变换中一行元素的乘加次数；
- $N\in(0,su*su)$ 表示输出变换中一行元素的乘加次数。

考虑到转换矩阵的稀疏性（即存在0和1（-1）），因此上面的 $M$ 和 $N$ 值与 Unit的选取相关且为定值。至于Uint如何确定，放到下一篇来讲。

根据对不同 $u$ ， $IC$ ， $OC$ 遍历实测，就乘加次数而言，仅当 $IC或OC≤2$ 的个别情况下（实际应用中，通道<=2的卷积情况非常少），Winograd在计算次数上是增加的，具体可以通过下面的代码简单验证。

void UnitTest(const int unit, const int &st, const int &dt, const int &ic, const int &oc, std::ofstream &fout, int kernel = 3) {
    float original_cost = (float)(2 * ic * kernel * kernel - 1) * oc;
    float src_transform_cost = 2 * (unit + kernel - 1) * st * ic;
    float matmul_cost = (unit + kernel - 1) * (unit + kernel - 1) * ic * oc;
    float dst_transform_cost = (2 * unit + kernel - 1) * dt * oc;
    float winograd_cost = (src_transform_cost + matmul_cost + dst_transform_cost) / (unit * unit);
    float rate = original_cost / winograd_cost;
    if (rate < 1) {
        printf("uint: %d, ic: %d, oc: %d, rate: %f\n", unit, ic, oc, rate);
    }
    fout << "unit:" << unit << ", ic:" << ic << ", oc:" << oc << ", rate:" << rate << std::endl;
}
 
void WinogradUnitTest3x3() {
    std::vector<int> u = { 2, 4, 6 };
    // mul + add
    std::vector<int> st = { 0 + 4, 10 + 16, 30 + 36 };
    std::vector<int> dt = { 0 + 4, 2 + 11, 10 + 32 };
    std::ofstream fout("unit_info.txt");
    // unit
    for (int k = 0; k < u.size(); ++k) {
        // input channel
        for (int i = 1; i <= 64; ++i) {
            // output channel
            for (int j = 1; j <= 64; ++j) {
                UnitTest(u[k], st[k], dt[k], i, j, fout);
            }
        }
    }
    fout.close();
}