前言

GEMM（General Matrix Multiplication，通用矩阵乘）是深度学习或其他涉及科学计算领域中常用的计算操作，也是消耗计算资源较大的操作，对其做性能优化就很有必要。

基本概念

$\begin{align*} C&=AB \quad A,B\in R^{n×n} \\ C_{m,n}&=\sum_{k=1}^KA_{m,k}B_{k,n} \quad m,n,k \in R^n \end{align*}$

其中 $A$ 、 $B$ 、 $C$ 的尺寸分别为 $M×K$ 、 $K×N$ 、 $M×N$ 。如下图所示：

基础实现（伪）代码如下：

for (int m = 0; m < M; m++) {
  for (int n = 0; n < N; n++) {
    C[m][n] = 0;
    for (int k = 0; k < K; k++) {
      C[m][n] += A[m][k] * B[k][n];
    }
  }
}

注意我们这里与how to optimize gemm保持一致，采用列优先（column-major）顺序存储矩阵元素。即元素 $A[m][k]$ 的索引值为 $k×M+m$ 。

对于GEMM性能的优化可以从两个方面入手：

1. 算法分析角度：根据矩阵乘计算特性，从数学角度优化，如前面提到的Strassen算法和Winograd算法，有兴趣可以传送过去，这里不再赘述；
1. 软件优化角度：根据计算机体系结构的特点，选择性的调整计算顺序，主要有循环拆分向量化和内存重排等，后续将以how to optimize gemm为参考展开讲。

How to optimize gemm

在考虑优化方法前，我们先看一下基础实现方法的计算操作数和访存量情况（不考虑 $C$ 矩阵初始化为0的操作）：

计算操作数： $2MNK$ ，其中 $M$ 、 $N$ 、 $K$ 分别为3层循环次数，2为最内层循环的1次乘法和1次加法；
访存量： $4MNK$ ，其中 $M$ 、 $N$ 、 $K$ 分别为3层循环次数，4为最内层循环中对 $C$ 、 $A$ 、 $B$ 中元素的内存访问次数， $C$ 先读后写，所以要2次。

这里我们将最内层循环称为微内核（micro kernel），后面可能会混用这两个概念。

how to optimize gemm中分步骤详细阐述了优化思路，最终的优化提升情况如下图所示：

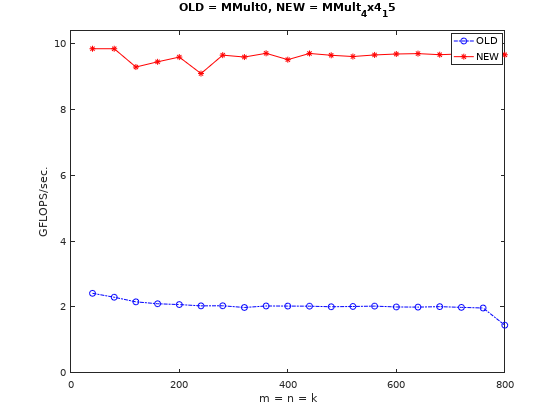
其核心思想就是将输出分块，进行计算拆分，以提高对输入的重用，减少访存。下面对其中几次关键提升展开来探讨一下（原文也介绍了一些无优化或负优化的操作，如循环展开、间接寻址代替指针递增、过多的使用普通寄存器等，这里不展开，有兴趣自己可以看下)。

`1 × 4`向量化

基础实现

首先how to optimize gemm中第一次明显的优化提升出现在这里，把输出的计算按列拆分成若干个 $1×4$ 的小块，最内层循环一次计算4个值，如下图：

gemm-1x4

实现的（伪）代码如下：

for (int n = 0; n < N; n += 4) {
  for (int m = 0; m < M; m++) {
    C[m][n + 0] = 0;
    C[m][n + 1] = 0;
    C[m][n + 2] = 0;
    C[m][n + 3] = 0;
    for (int k = 0; k < K; k++) {
      C[m][n + 0] += A[m][k] * B[k][n + 0];
      C[m][n + 1] += A[m][k] * B[k][n + 1];
      C[m][n + 2] += A[m][k] * B[k][n + 2];
      C[m][n + 3] += A[m][k] * B[k][n + 3];
    }
  }
}

按照原文的解释是这里最内层循环中 $A[m][k]$ 元素是可以重用的，只需从内存中加载一次就可以供给4次运算。但这里其实在代码中是没有体现的，之所以还能奏效全仰仗编译器的优化能力（即编译器能够在编译优化时将上述代码中的 $A[m][k]$ 加载到某一固定寄存器中以实现4次数据复用）。因此该实现的访存量变为了 $(2+1+\frac{1}{4})MNK$ 。

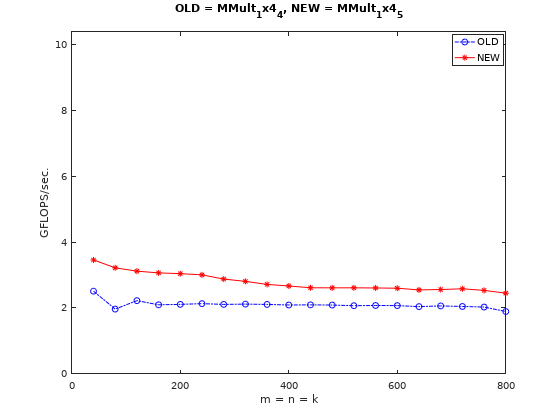
进一步优化：使用寄存器减少访存

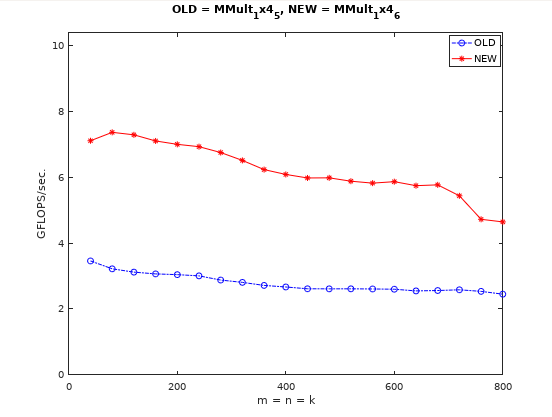
这一步性能有了进一步的优化，主要有两点修改：

作者明确使用了1个寄存器代替了循环中的 $A[m][k]$ ，一次加载，4次复用，与上一轮优化的目标是一致的，但是只做这一修改的性能相比之前靠编译器完成复用优化的版本还是有一定幅度的性能提升，说明单纯依赖编译器优化并不可靠。
作者用4个寄存器代替了循环中的 $C[m][n+0..3]$ ，累加计算先写到寄存器中，等最内层循环结束后再写到 $C$ 矩阵对应位置的内存中， $C$ 矩阵中每个元素只需写1次。因此我们的访存量变为了 $MN+(1+\frac{1}{4})MNK$ 。

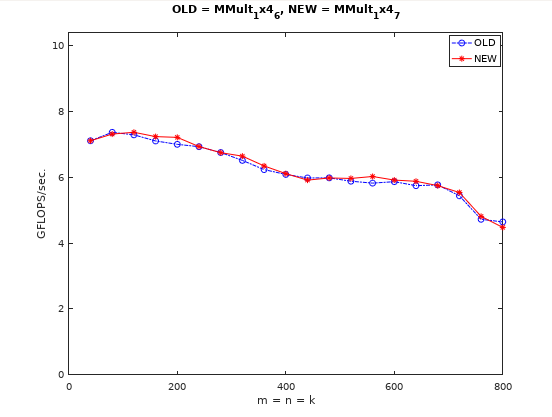
进一步优化：使用指针减少索引开销

这一步用指针指向了 $B[k][n + 0..3]$ 的首地址，在微内核中只需递增指针即可完成 $B$ 的遍历，而不需要计算索引值（一般内存存储并不像伪代码中的二维形式，而是一维的， $B[k][n]$ 的索引值 $nK+k$ 每次都要计算）。原文中这一步是有优化收益的，但我实测下来性能提升并不明显（可能跟编译器的优化或指令集不同有关吧）。

`4 × 4`向量化

基础实现

与 $1 × 4$ 向量化类似，这里把输出的计算按列拆分成若干个 $4×4$ 的小块，最内层循环一次计算16个值，如下图所示：

gemm-4x4

实现的（伪）代码可以写成：

for (int n = 0; n < N; n += 4) {
  for (int m = 0; m < M; m += 4) {
    C[m + 0][n + 0..3] = 0;
    C[m + 1][n + 0..3] = 0;
    C[m + 2][n + 0..3] = 0;
    C[m + 3][n + 0..3] = 0;
    for (int k = 0; k < K; k++) {
      C[m + 0][n + 0..3] += A[m + 0][k] * B[k][n + 0..3];
      C[m + 1][n + 0..3] += A[m + 1][k] * B[k][n + 0..3];
      C[m + 2][n + 0..3] += A[m + 2][k] * B[k][n + 0..3];
      C[m + 3][n + 0..3] += A[m + 3][k] * B[k][n + 0..3];
    }
  }
}

这里微内核中的 $A[m + 0..3][k]$ 和 $B[k][n + 0..3]$ 都是可以复用的。即在 $1 × 4$ 向量化的基础上减少了 $B$ 的访存量。在不考虑其他进一步优化操作的情况下，访存量变为了 $(2+\frac{1}{4}+\frac{1}{4})MNK$ 。与未做任何优化对比如下：

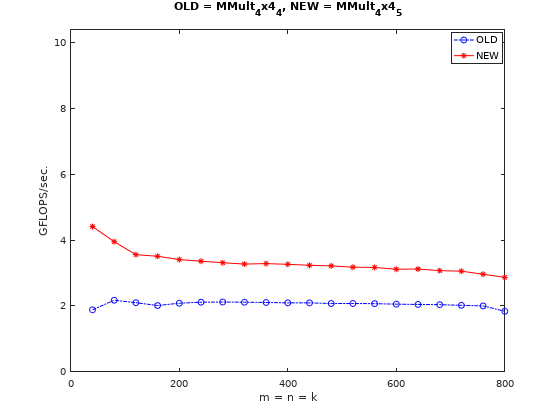
与 $1 × 4$ 向量化的基础实现对比如下:

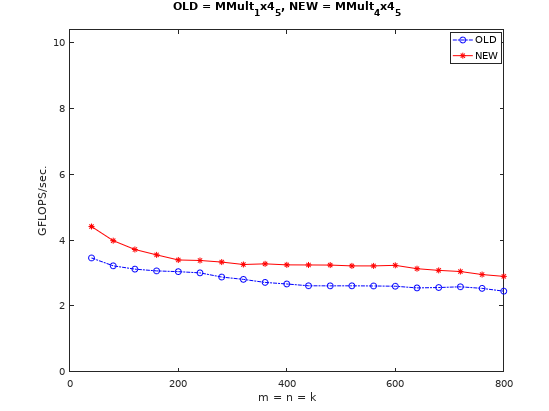
进一步优化

同样的，使用寄存器减少访存能够减少 $C$ 的访存量，将总的访存量减少到 $MN+(\frac{1}{4}+\frac{1}{4})MNK$ ，从而获得性能提升，这是可以预见的。

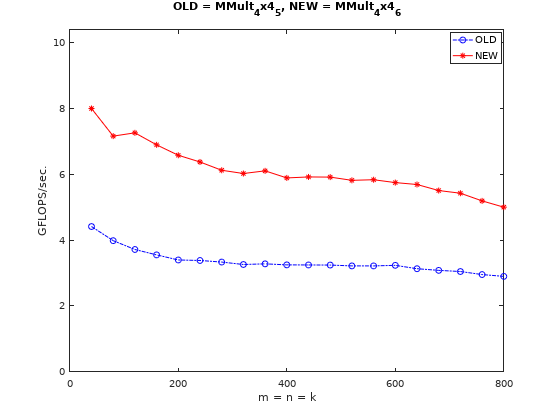
但是与相同优化策略下的 $1 × 4$ 向量化测试用例MMult_1x4_6对比，实测下来并没有与文中那样更有优势，可能使用的普通寄存器太多，反而起到了负优化。

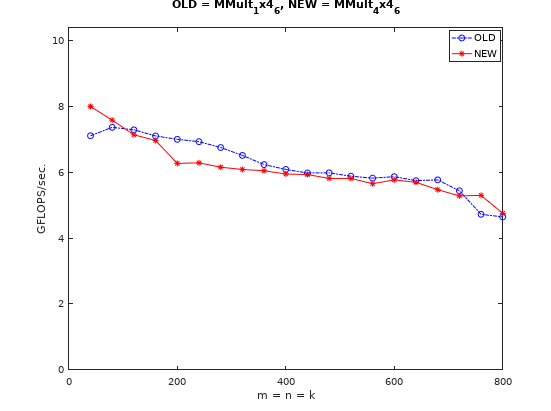
同样的，使用指针减少索引开销的性能提升也不明显。

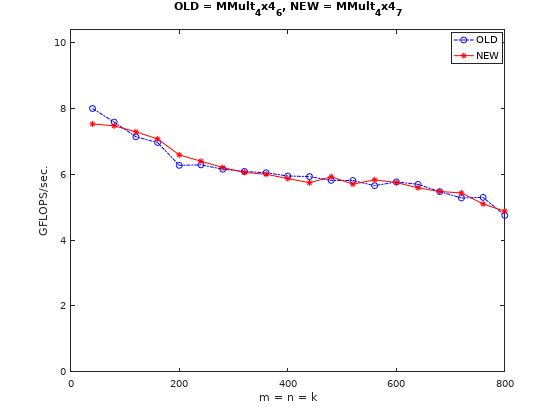
更进一步优化：SIMD

这一步开始使用SSE指令进行并行计算加速，由于数据类型为double，128位的向量寄存器的并行度为2。实测下来也和预期一样，性能提升明显。

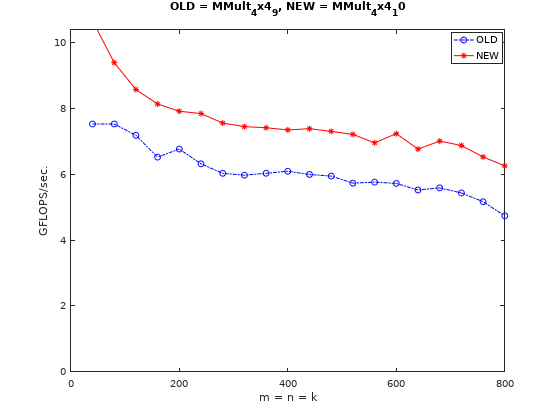
更进一步优化：大矩阵分块

从前面图中也可以看出，随着矩阵尺寸的增大，性能是会下降的。这主要是因为随着尺寸的增大， $A$ 矩阵这种跳列的非连续访问的矩阵（假设是列优先存储）cache miss的情况会越来越严重。

大矩阵分块的目的就是解决cache miss。

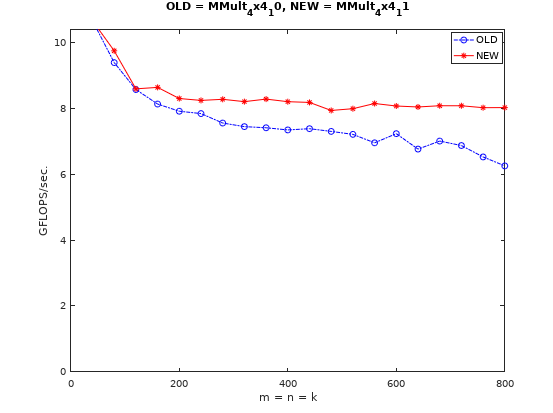
更进一步优化：优化局部内存布局

从上图中可以看到，虽然尺寸＞200之后的性能下降止住了，但是1-200之间还是会有性能下降。这还是因为不能命中L1 Cache的原因导致的。

因此可以通过优化 $A$ 矩阵的局部内存布局来提高L1 Cache命中。如下图所示：

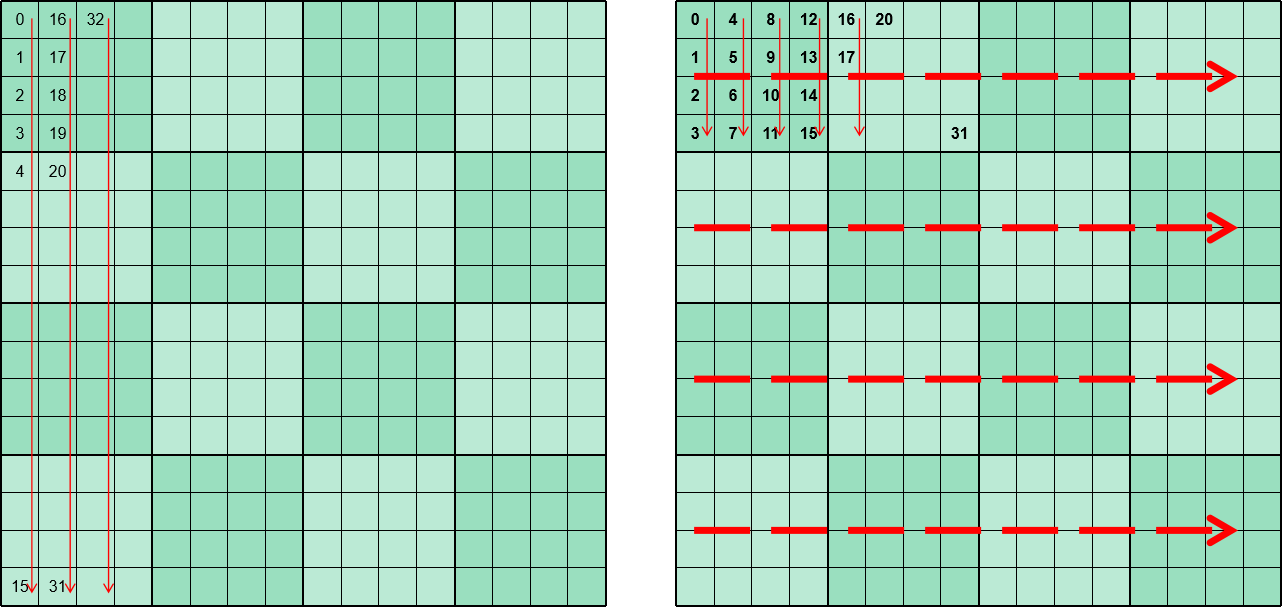
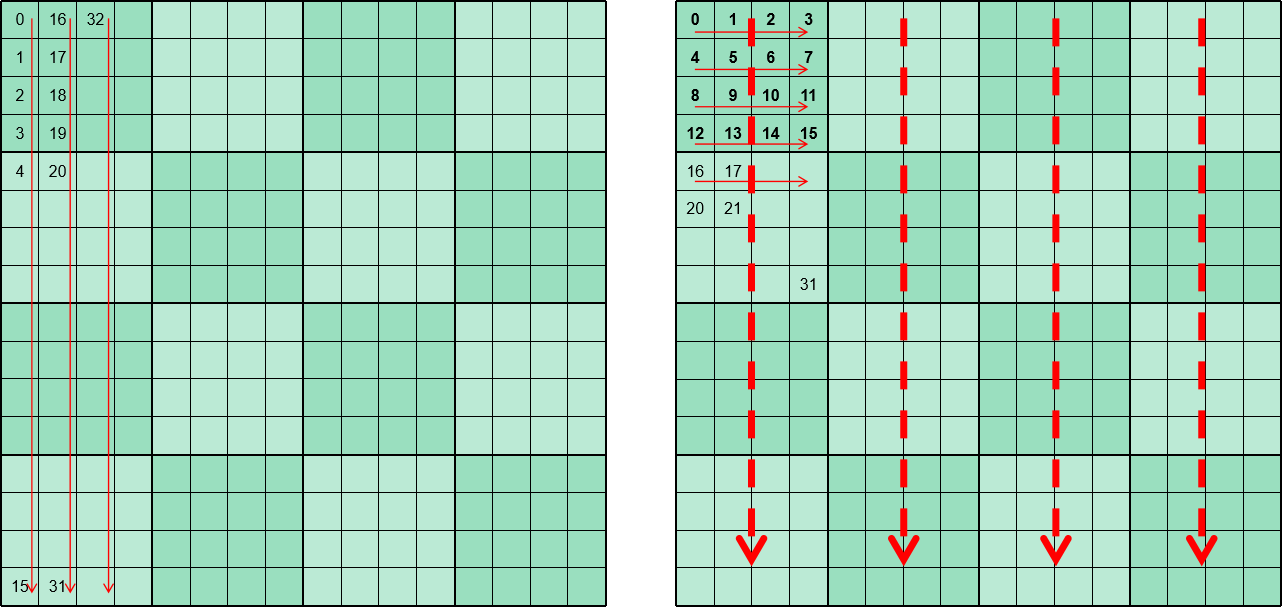
假设依然是列优先存储，微内核大小为4 x 4，计算方向是 $K$ 方向，即 $A$ 矩阵的水平方向，每次循环加载4个元素后，就需要跳到下一列去加载4个元素。假设Cache Line Size 为64Byte，数据元素大小为8byte，则执行一次访存操作会将8个元素读到Cache中。

$A$ 矩阵普通的内存排布顺序就如左侧红色箭头所示。每次访存load到Cache Line中实际只需要前四个值，后四个值暂时不会用。当 $A$ 的列数 $K$ 小的时候， $K$ 循环结束时L1 Cache还没被填满，则每个Cache Line的后四个值还能命中。但当 $A$ 的列数足够大时，后四个值还没被用Cache就满了，最早load的Cache Line会被覆盖，当你真正要用后四个值的时候还得重新load，这就是发生了L1 Cache miss。
而采用右侧这样的内存排布，微内核依次加载的内存是连续的，一次load到Cache Line中8个值会在连续的两次运算中被用到，这就减少来Cache miss，从而提高了性能。

优化局部内存布局的性能对比情况如下图：

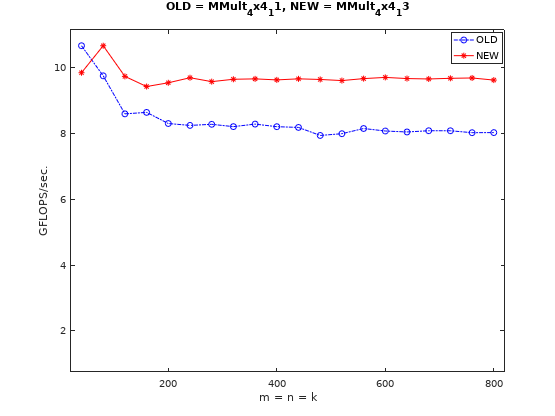
同样的也可以对 $B$ 矩阵的局部内存排布做优化，如下图：

但是实测下来，与原文所述表现不同的是，对 $B$ 矩阵的局部内存排布的优化并没有取得明显的提升，反而出现了一定程度的负优化。

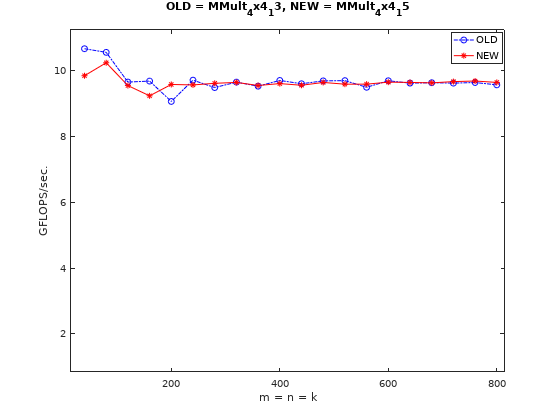
这可能跟 $B$ 矩阵元素的取用顺序有关，对 $B$ 而言，微内核的方向（即 $K$ ）的方向是垂直方向，每次取完水平方向的4个元素后，会跳到下一行继续取用。

从整个L1 Cache的角度看，一次微内核中内存块只有 $4*K$ 大小，以测试中 $K_{max}=800$ ，单个元素为8Byte为例，则大小为 $4*800*8/1024=25KB$ ，并没有超过我的电脑的L1 Cache大小（32KB）。
从Cache Line的角度看，即使是上图左侧的内存排布方式，一次load到Cache Line中的8个值（Cache Line Size = 64B，DataType=double）中的后4个值虽然不会在下一次load前就马上被用掉，但也就隔3次load后就会被用到，所以不会出现L1 Cache miss。

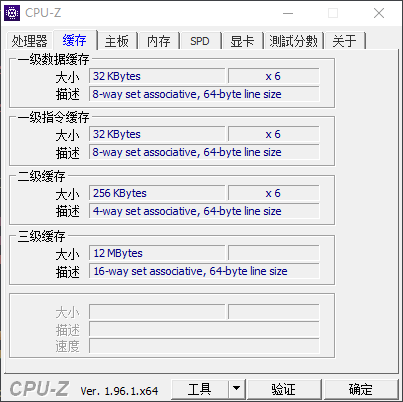
因此对 $B$ 矩阵的局部排布优化没有起到预期的效果，反而因为局部内存重排本身的计算代价（这里作者是将 $B$ 矩阵的重排操作放在了运行时计算中，对于实际的神经网络而言， $B$ 对应权重，是固定不变的。所以是可以在运行时前的初始化阶段完成重排操作的）导致出现负优化。至于原文中作者为什么能有性能提升，闹不明白（按照作者的描述，他用的1.7Ghz Intel Core i5的MacBook Air，查了下对应的CPU是I5-2557M，其L1 Cache 大小是64KB，这就说不太通了）。

QNNPACK

QNNPACK（Quantized Neural Network PACKage）是Facebook 开源的专门用于量化神经网络的计算加速库。是在 NNPACK (Neural Network PACKage) 的基础上，在量化（Quantization）技术被引入到神经网络中后进一步优化的计算加速库。

QNNPACK 开源时附带了一份技术报告性质的博客。其中也描述了QNNPACK对于GEMM优化的思路，与传统方法略有区别，但大同小异。归纳一下，就是针对在移动端运行的量化后的神经网络这一特定应用领域，对微内核尺寸和局部内存重排方式做了特定的处理，以获得更好的性能。